Paper:
Dual-Level Template for Enhancing Resolution of Quantum Images
Shan Zhao*1, Fei Yan*1,†, Abdullah M. Iliyasu*2,*3, Ahmed S. Salama*4, and Kaoru Hirota*3,*5
*1School of Computer Science and Technology, Changchun University of Science and Technology
Changchun 130022, China
Al-Kharj 11942, Saudi Arabia
*3School of Computing, Tokyo Institute of Technology
Yokohama 226-8502, Japan
*4Faculty of Engineering and Technology, Future University in Egypt
New Cairo 11845, Egypt
*5School of Automation, Beijing Institute of Technology
Beijing 100081, China
†Corresponding author
Quantum information science is an emerging research field devoted to the use of quantum mechanical systems to devise and implement information processing tasks faster than that possible with classical computers. In this study, two quantum image resolution enhancement (QIRE-I and QIRE-II) schemes are proposed based on quantum wavelet transform and quantum interpolation. Using these, the resolutions of low-resolution (LR) images are enhanced by decomposing them into four frequency sub-bands using a single-level one-dimensional (1-D) quantum Haar wavelet transform (QHWT). Subsequently, to preserve the edges and obtain sharper high-resolution (HR) images, quantum interpolation was applied to three of the high-frequency sub-bands. A few simulation-based demonstrations are presented to illustrate the feasibility and effectiveness of the proposed schemes. The visual and quantitative results demonstrate the superiority of the proposed schemes over those that use only quantum interpolation.
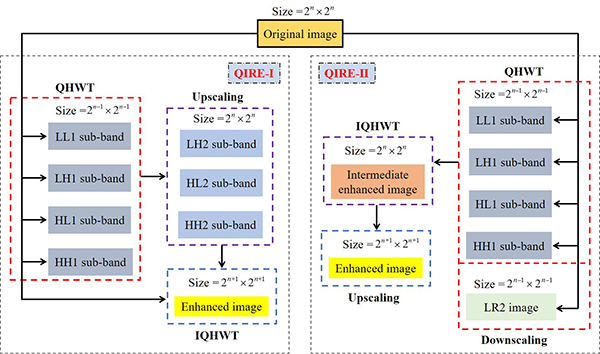
Block diagram for the two QIRE schemes
- [1] C. H. Bennett and D. P. DiVincenzo, “Quantum information and computation,” Nature, Vol.404, No.6775, pp. 247-255, 2000.
- [2] D. Deutsch and R. Jozsa, “Rapid solution of problems by quantum computation,” Proc. of the Royal Society of London. Series A: Mathematical and Physical Sciences, Vol.439, No.1907, pp. 553-558, 1992.
- [3] P. W. Shor, “Algorithms for quantum computation: Discrete logarithms and factoring,” Proc. of the 35th Annual Symp. on Foundations of Computer Science, pp. 124-134, 1994.
- [4] L. K. Grover, “A fast quantum mechanical algorithm for database search,” Proc. of the 28th Annual ACM Symp. on Theory of Computing, pp. 212-219, 1996.
- [5] F. Yan and S. E. Venegas-Andraca, “Quantum Image Processing,” Springer, 2020.
- [6] A. Y. Vlasov, “Quantum computations and images recognition,” arXiv: Quantum Physics, 1997.
- [7] A. M. Iliyasu, “Towards realising secure and efficient image and video processing applications on quantum computers,” Entropy, Vol.15, No.8, pp. 2874-2974, 2013.
- [8] P. Q. Le, F. Dong, and K. Hirota, “A flexible representation of quantum images for polynomial preparation, image compression, and processing operations,” Quantum Information Processing, Vol.10, No.1, pp. 63-84, 2011.
- [9] Y. Zhang, K. Lu, Y. Gao, and M. Wang, “NEQR: A novel enhanced quantum representation of digital images,” Quantum Information Processing, Vol.12, No.8, pp. 2833-3126, 2013.
- [10] B. Sun, A. M. Iliyasu, F. Yan et al., “An RGB multi-channel representation for images on quantum computers,” J. Adv. Comput. Intell. Intell. Inform., Vol.17, No.3, pp. 404-417, 2013.
- [11] P. Q. Le, A. M. Iliyasu, F. Dong, and K. Hirota, “Fast geometric transformations on quantum images,” Int. J. of Applied Mathematics, Vol.40, No.3, pp. 113-123, 2010.
- [12] P. Q. Le, A. M. Iliyasu, F. Dong, and K. Hirota, “Efficient color transformations on quantum image,” J. Adv. Comput. Intell. Intell. Inform., Vol.15, No.6, pp. 698-706, 2011.
- [13] A. M. Iliyasu, P. Q. Le, F. Dong, and K. Hirota, “Watermarking and authentication of quantum images based on restricted geometric transformations,” Information Sciences, Vol.186, pp. 126-149, 2012.
- [14] F. Yan, A. M. Iliyasu, and S. E. Venegas-Andraca, “A survey of quantum image representations,” Quantum Information Processing, Vol.15, pp. 1-35, 2016.
- [15] F. Yan, A. M. Iliyasu, and P Q. Le, “Quantum image processing: A review of advances in its security technologies,” Int. J. of Quantum Information, Vol.15, No.3, Article No.1730001, 2017.
- [16] S. Zhao, F. Yan, and K. Hirota, “Quantum image resolution enhancement based on quantum wavelet transform and interpolation,” 7th Int. Workshop on Advanced Computational Intelligence and Intelligent Informatics (IWACIII), pp. 1-6, 2021.
- [17] A. Polesel, R. Giovanni, and V. J. Mathews, “Image enhancement via adaptive unsharp masking,” IEEE Trans. on Image Processing, Vol.9, No.3, pp. 505-510, 2000.
- [18] R. Gonzalez and R. Woods, “Digital Image Processing 3rd Edition,” Pearson Education, 2008.
- [19] Y. Piao, L. Shin, and H. Park, “Image resolution enhancement using inter-subband correlation in wavelet domain,” Proc. of the IEEE Int. Conf. on Image Processing, pp. 445-448, 2007.
- [20] B. R. V. S. Narayana and K. Nirmala, “Image resolution enhancement by using stationary and discrete wavelet decomposition,” Int. J. of Image, Graphics and Signal Processing, Vol.4, No.11, pp. 41-46, 2012.
- [21] A. Fijany and C. P. Williams, “Quantum wavelet transforms: Fast algorithms and complete circuits,” NASA Int. Conf. on Quantum Computing and Quantum Communications, pp. 10-33, 1998.
- [22] F. Kou, W. Chen, Z. Li, and C. Wen, “Content adaptive image detail enhancement,” IEEE Signal Processing Letters, Vol.22, No.2, pp. 211-215, 2015.
- [23] S. G. Chang, Z. Cvetkovic, and M. Vetterli, “Resolution enhancement of images using wavelet transform extrema extrapolation,” Proc. of the IEEE Int. Conf. on Acoustics, Speech, and Signal Processing, Vol.4, pp.2379-2382, 1995.
- [24] K. Kinebuchi, D. D. Muresan, and T. W. Parks, “Image interpolation using wavelet-based hidden Markov trees,” Proc. of the IEEE Int. Conf. on Acoustics, Speech, and Signal Processing, Vol.3, pp. 1957-1960, 2001.
- [25] P. Hoyer, “Efficient quantum transform,” arXiv: Quantum Physics, 1997.
- [26] P. Q. Le, A. M. Iliyasu, F. Dong, and K. Hirota, “A flexible representation and invertible transformations for images on quantum computers,” A. E. Ruano and A. R. Várkonyi-Kóczy (Eds.), New Advances in Intelligent Signal Processing, Vol.372, pp. 179-202, 2011.
- [27] F. Yan, S. Zhao, S. E. Venegas-Andraca, and K. Hirota, “Implementing bilinear interpolation on quantum images,” Digital Signal Processing, Vol.117, Article No.103149, 2021.
- [28] J. Sang, S. Wang, and X. Niu, “Quantum realization of the nearest-neighbor interpolation method for FRQI and NEQR,” Quantum Information Processing, Vol.15, pp. 37-64, 2016.
- [29] H. Li, P. Fan, H.-Y. Xia, and S. Song, “Quantum multi-level wavelet transforms,” Information Sciences, Vol.504, pp. 113-135, 2019.
- [30] H.-S. Li, P. Fan, H. Peng, S. Song, and G.-L. Long, “Multilevel 2-D quantum wavelet transforms,” IEEE Trans. on Cybernetics, doi: 10.1109/TCYB.2021.3049509, 2021.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.