Paper:
A Memetic Algorithm for High-Speed Railway Train Timetable Rescheduling
Shuxin Ding*1,*2, Tao Zhang*1,*2,†, Ziyuan Liu*3, Rongsheng Wang*1,*2,*4, Sai Lu*5,*6, Bin Xin*5,*6, and Zhiming Yuan*1,*2
*1Signal and Communication Research Institute, China Academy of Railway Sciences Co., Ltd.
No.2 Daliushu Road, Haidian District, Beijing 100081, China
*2Train Operation Control Laboratory for High-Speed Railway,
National Engineering Research Center of System Technology for High-Speed Railway and Urban Rail Transit,
China Academy of Railway Sciences Co., Ltd.
No.2 Daliushu Road, Haidian District, Beijing 100081, China
*3China Academy of Railway Sciences Co., Ltd.
No.2 Daliushu Road, Haidian District, Beijing 100081, China
*4Postgraduate Department, China Academy of Railway Sciences
No.2 Daliushu Road, Haidian District, Beijing 100081, China
*5School of Automation, Beijing Institute of Technology
No.5 Zhongguancun South Street, Haidian District, Beijing 100081, China
*6State Key Laboratory of Intelligent Control and Decision of Complex Systems, Beijing Institute of Technology
No.5 Zhongguancun South Street, Haidian District, Beijing 100081, China
†Corresponding author
This study addresses a high-speed railway train timetable rescheduling (TTR) problem with a complete blockage at the station and train operation constraints. The problem is formulated as a mixed-integer linear programming (MILP) model that minimizes the weighted sum of the total delay time of trains. A memetic algorithm (MA) is proposed, and the individual of MA is represented as a permutation of trains’ departure order at the disrupted station. The individual is decoded to a feasible schedule of the trains using a rule-based method to allocate the running time in sections and dwell time at stations. Consequently, the original problem is reformulated as an unconstrained problem. Several permutation-based operators are involved, including crossover, mutation, and local search. A restart strategy was employed to maintain the the population diversity. The proposed MA was compared with the first-scheduled-first-served (FSFS) algorithm and other state-of-the-art evolutionary algorithms. The experimental results demonstrate the superiority of MA in solving the TTR through permutation-based optimization in terms of constraint handling, solution quality, and computation time.
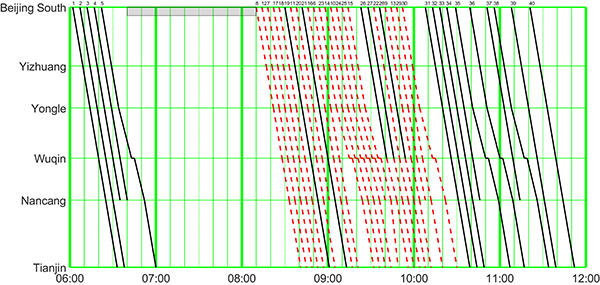
Rescheduled train timetable
- [1] M. Zhou, H. Dong, X. Liu, H. Zhang, and F.-Y. Wang, “Integrated timetable rescheduling for multidispatching sections of high-speed railways during large-scale disruptions,” IEEE Trans. Comput. Soc. Syst., Vol.9, No.2, pp. 366-375, 2021.
- [2] V. Cacchiani, D. Huisman, M. Kidd, L. Kroon, P. Toth, L. Veelenturf, and J. Wagenaar, “An overview of recovery models and algorithms for real-time railway rescheduling,” Transp. Res. Part B: Methodol., Vol.63, pp. 15-37, 2014.
- [3] W. Fang, S. Yang, and X. Yao, “A survey on problem models and solution approaches to rescheduling in railway networks,” IEEE Trans. Intell. Transp. Syst., Vol.16, No.6, pp. 2997-3016, 2015.
- [4] S. Zhan, L. G. Kroon, L. P. Veelenturf, and J. C. Wagenaar, “Real-time high-speed train rescheduling in case of a complete blockage,” Transp. Res. Part B: Methodol., Vol.78, pp. 182-201, 2015.
- [5] S. Ding, C. Chen, Q. Zhang, B. Xin, and P. M. Pardalos, “Metaheuristics for Resource Deployment Under Uncertainty in Complex Systems,” CRC Press, 2021.
- [6] M. Wang, L. Wang, X. Xu, Y. Qin, and L. Qin, “Genetic algorithm-based particle swarm optimization approach to reschedule high-speed railway timetables: A case study in China,” J. Adv. Transp., Article No.6090742, 2019.
- [7] X. Meng, Y. Wang, W. Xiang, and L. Jia, “An integrated model for train rescheduling and station track assignment,” IET Intell. Transp. Syst., Vol.15, Issue 1, pp. 17-30, 2021.
- [8] R. Wang, M. Zhou, Y. Li, Q. Zhang, and H. Dong, “A timetable rescheduling approach for railway based on Monte Carlo tree search,” Proc. IEEE Intell. Transp. Syst. Conf. (ITSC), pp. 3738-3743, 2019.
- [9] S. Wang and L. Wang, “An effective estimation of distribution algorithm for multi-track train scheduling problem,” Int. Conf. Intell. Comput. (ICIC2014), Vol.8589, pp. 697-708, 2014.
- [10] S. Ding, T. Zhang, R. Wang, C. Zhang, S. Lu, and B. Xin, “A comparative study on evolutionary algorithms for high-speed railway train timetable rescheduling problem,” 7th Int. Work. Adv. Comput. Intell. Intell. Informatics (IWACIII2021), Article No.T2-1-6, 2021.
- [11] F. Neri and C. Cotta, “Memetic algorithms and memetic computing optimization: A literature review,” Swarm Evol. Comput., Vol.2, pp. 1-14, 2012.
- [12] Y. Wang, B. Xin, L. Dou, and Z. Peng, “A heuristic initialized memetic algorithm for the joint allocation of heterogeneous stochastic resources,” IEEE Congr. Evol. Comput. (CEC), pp. 1929-1936, 2019.
- [13] Y. Ding, B. Xin, H. Zhang, and J. Chen, “A memetic algorithm for curvature-constrained path planning of messenger UAV in air-ground coordination,” IEEE Int. Conf. Syst. Man, Cybern. (SMC), pp. 1465-1472, 2020.
- [14] G. Gao, Y. Mei, B. Xin, Y.-H. Jia, and W. Browne, “A memetic algorithm for the task allocation problem on multi-robot multi-point dynamic aggregation missions,” IEEE Congr. Evol. Comput. (CEC), 2020.
- [15] Y. Wang, B. Xin, and J. Chen, “An adaptive memetic algorithm for the joint allocation of heterogeneous stochastic resources,” IEEE Trans. Cybern., 2021.
- [16] A. J. Umbarkar and P. D. Sheth, “Crossover operators in genetic algorithms: A review,” ICTACT J. Soft Comput., Vol.6, No.1, pp. 1083-1092, 2015.
- [17] J. Lofberg, “YALMIP: a toolbox for modeling and optimization in MATLAB,” Int. Conf. on Robotics and Automation, pp. 284-289, 2004.
- [18] S. Lu and B. Xin, “Tabu-model-based estimation of distribution algorithm framework for permutation optimization problems,” 9th Int. Symp. Comput. Intell. Ind. Appl. (ISCIIA2020), Article No.1A2-2-2, 2020.
- [19] J. J. Liang, A. K. Qin, P. N. Suganthan, and S. Baskar, “Comprehensive learning particle swarm optimizer for global optimization of multimodal functions,” IEEE Trans. Evol. Comput., Vol.10, No.3, pp. 281-295, 2006.
- [20] N. Hansen and A. Ostermeier, “Adapting arbitrary normal mutation distributions in evolution strategies: the covariance matrix adaptation,” Proc. IEEE Int. Conf. Evol. Comput., pp. 312-317, 1996.
- [21] S. Mirjalili, “Genetic Algorithm,” “Evolutionary algorithms and neural networks,” pp. 43-55, Springer, 2019.
- [22] S. Ding, R. Wang, X. Zhou, Y. Ren, and K. Huang, “High-speed railway train timetable rescheduling in case of a stochastic section blockage,” Chinese Autom. Congr. (CAC), pp. 4322-4327, 2021.
- [23] S. Ding, C. Chen, B. Xin, and P. M. Pardalos, “A bi-objective load balancing model in a distributed simulation system using NSGA-II and MOPSO approaches,” Appl. Soft Comput., Vol.63, pp. 249-267, 2018.
- [24] W. Zheng, Y. Tan, M. Gao, W. Jia, and Q. Wang, “A modification of MOEA/D for solving multi-objective optimization problems,” J. Adv. Comput. Intell. Intell. Inform., Vol.22, No.2, pp. 214-223, 2018.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.