Paper:
Evolutionary Computation System Solving Group Decision Making Multiobjective Problems for Human Groups
Hironao Sakamoto, Kotaro Nakamoto, and Kei Ohnishi
Graduate School of Computer Science and Systems Engineering, Kyushu Institute of Technology
680-4 Kawazu, Iizuka, Fukuoka 820-8502, Japan
In a previous work, we proposed an evolutionary computation system designed to solve group decision making multiobjective problems for human groups, which is equivalent to obtaining consensus solutions to multiobjective optimization problems. Multi-human-agent-based evolutionary computation (Mhab-EC) is a primary component of the system, used to obtain converged solutions for multiobjective optimization problems. The other main component is a mechanism that allows owners of simulated human agents to review simulation results thus far and adjust their agents accordingly between successive simulation runs of the Mhab-EC. However, in our previous study, we simply conducted simulations to demonstrate that a single run yielded converged solutions. Consensus solutions were assumed to be obtained through iterations of the Mhab-EC run and agent adjustment. Therefore, in this study, we conducted simulations of the entire system, including the agent adjustment mechanism. For this purpose, we implemented a simple model of agent adjustment by owners to facilitate solution convergence. Simulation results showed that the system indeed yielded converged solutions, which are considered to indicate consensus.
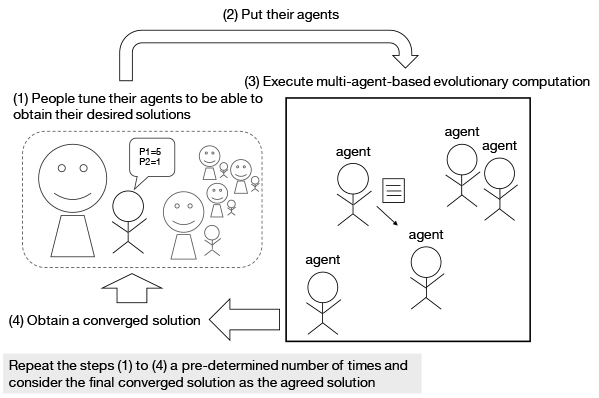
Problem-solving system for human groups
- [1] K. Deb, “Multi-Objective Optimization Using Evolutionary Algorithms,” John Wiley & Sons, Inc., 2001.
- [2] H. Sakamoto, K. Nakamoto, and K. Ohnishi, “Acquiring Consensus Solutions by Multi-human-agent-based Evolutionary Computation,” 2021 5th IEEE Int. Conf. on Cybernetics (CYBCONF), doi: 10.1109/CYBCONF51991.2021.9464147, 2021.
- [3] K. Nag, T. Pal, R. Mudi, and N. Pal, “Robust Multiobjective Optimization with Robust Consensus,” IEEE Trans. on Fuzzy Systems, Vol.26, No.6, pp. 3743-3754, 2018.
- [4] L. Thiele, K. Miettinen, P. J. Korhonen, and J. Molina, “A Preference-Based Evolutionary Algorithm for Multi-Objective Optimization,” Evolutionary Computation, Vol.17, No.3, pp. 411-436, 2009.
- [5] K. Li, M. Liao, K. Deb, G. Min, and X. Yao, “Does Preference Always Help? A Holistic Study on Preference-Based Evolutionary Multiobjective Optimization Using Reference Points,” IEEE Trans. on Evolutionary Computation, Vol.24, No.6, pp. 1078-1096, 2020.
- [6] A. Byrski, R. Drezewski, L. Siwik, and M. Kisiel-Dorohinicki, “Evolutionary multi-agent systems,” The Knowledge Engineering Review, Vol.30, No.2, pp. 171-186, 2015.
- [7] A. S. Akopov and M. A. Hevencev, “A Multi-agent Genetic Algorithm for Multi-objective Optimization,” 2013 IEEE Int. Conf. on Systems, Man, and Cybernetics, pp. 1391-1395, 2013.
- [8] R. Tanese, “Distributed Genetic Algorithms,” Proc. of the 3rd Int. Conf. on Genetic Algorithms, pp. 434-439, 1989.
- [9] B. Manderick and P. Spiessens, “Fine-Grained Parallel Genetic Algorithms,” Proc. of the 3rd ICGA, pp. 428-433, 1989.
- [10] R. Hasebe, K. Ohnishi, and M. Koeppen, “Distributed Human-based Genetic Algorithm Utilizing A Mobile Ad Hoc Network,” pp. 174–179, 2013.
- [11] K. Ohnishi, J. Okano, and M. Köppen, “Building a Simulation Model for Distributed Human-based Evolutionary Computation,” 2013 IEEE Int. Conf. on Cybernetics (CYBCO), pp. 40-49, 2017.
- [12] E. Zitzler and L. Thiele, “Multiobjective evolutionary algorithms: A comparative case study and the strength pareto approach,” IEEE Trans. on Evolutionary Computation, Vol.3, No.24, pp. 257-271, 1999.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.