Top > JACIII > Multilayer Batch Learning Growing Neural Gas for Learning Mult ...

single-jc.php

JACIII Vol.25 No.6 pp. 1011-1023
doi: 10.20965/jaciii.2021.p1011
(2021)

Paper:

Views over last 60 days: 551

Multilayer Batch Learning Growing Neural Gas for Learning Multiscale Topologies

Yuichiro Toda†, Takayuki Matsuno, and Mamoru Minami

Okayama University
3-1-1 Tsushima-Naka, Kita-Ku, Okayama, Okayama 700-8530, Japan

†Corresponding author

Received:
October 2, 2019
Accepted:
September 14, 2021
Published:
November 20, 2021
Creative Commons License
Keywords:
growing neural gas, hierarchical competitive learning, unsupervised learning
Abstract

Hierarchical topological structure learning methods are expected to be developed in the field of data mining for extracting multiscale topological structures from an unknown dataset. However, most methods require user-defined parameters, and it is difficult for users to determine these parameters and effectively utilize the method. In this paper, we propose a new parameter-less hierarchical topological structure learning method based on growing neural gas (GNG). First, we propose batch learning GNG (BL-GNG) to improve the learning convergence and reduce the user-designed parameters in GNG. BL-GNG uses an objective function based on fuzzy C-means to improve the learning convergence. Next, we propose multilayer BL-GNG (MBL-GNG), which is a parameter-less unsupervised learning algorithm based on hierarchical topological structure learning. In MBL-GNG, the input data of each layer uses parent nodes to learn more abstract topological structures from the dataset. Furthermore, MBL-GNG can automatically determine the number of nodes and layers according to the data distribution. Finally, we conducted several experiments to evaluate our proposed method by comparing it with other hierarchical approaches and discuss the effectiveness of our proposed method.

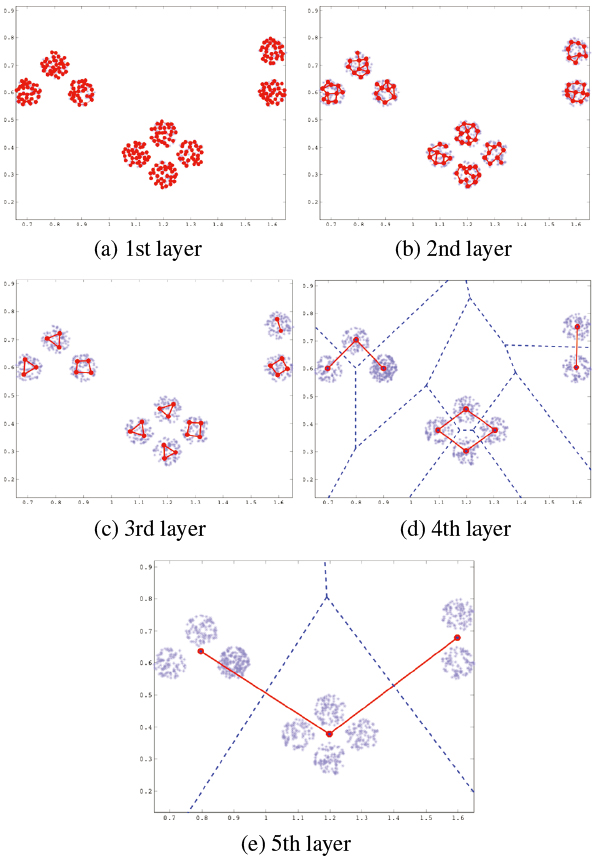
Results of MBL-GNG in 9C dataset. The blue and red dots indicate input data and nodes, respectively. The red line indicates the edge of MBL-GNG. In (d) and (e), blue dashed line indicates Voronoi edge

Results of MBL-GNG in 9C dataset. The blue and red dots indicate input data and nodes, respectively. The red line indicates the edge of MBL-GNG. In (d) and (e), blue dashed line indicates Voronoi edge

Cite this article as:
Y. Toda, T. Matsuno, and M. Minami, “Multilayer Batch Learning Growing Neural Gas for Learning Multiscale Topologies,” J. Adv. Comput. Intell. Intell. Inform., Vol.25 No.6, pp. 1011-1023, 2021.
Data files:
References
  1. [1] R. O. Duda, P. E. Hart, and D. G. Stork, “Pattern Classification,” 2nd edition, John Wiley & Sons, 2012.
  2. [2] D. V. Prokhorov, L. A. Feldkamp, and T. M. Feldkamp, “A new approach to cluster-weighted modeling,” Int. Joint Conf. on Neural Networks Proc. (IJCNN’01), 2001.
  3. [3] F. Nie, Z. Zeng, I. W. Tsang, D. Xu, and C. Zhang, “Spectral Embedded Clustering: A Framework for In-Sample and Out-of-Sample Spectral Clustering,” IEEE Trans. on Neural Networks, Vol.22, No.11, pp. 1796-1808, 2011.
  4. [4] H. Truong, L. Ngo, and L. Pham, “Interval Type-2 Fuzzy Possibilistic C-Means Clustering Based on Granular Gravitational Forces and Particle Swarm Optimization,” J. Adv. Comput. Intell. Intell. Inform., Vol.23, No.3, pp. 592-601, 2019.
  5. [5] Y. Hamasuna, S. Nakano, R. Ozaki, and Y. Endo, “Cluster Validity Measures Based Agglomerative Hierarchical Clustering for Network Data,” J. Adv. Comput. Intell. Intell. Inform., Vol.23, No.3, pp. 577-583, 2019.
  6. [6] M. Higashi, T. Kondo, and Y. Kanzawa, “Fuzzy Clustering Method for Spherical Data Based on q-Divergence,” J. Adv. Comput. Intell. Intell. Inform., Vol.23, No.3, pp. 561-570, 2019.
  7. [7] D. Heinke and F. H. Hamker, “Comparing neural networks: a benchmark on growing neural gas, growing cell structures, and fuzzy ARTMAP,” IEEE Trans. on Neural Networks, Vol.9, No.6, pp. 1279-1291, 1998.
  8. [8] B. Fritzke, “A growing neural gas network learns topologies,” Advances in Neural Information Processing Systems 7: Proc. of the 1994 Conf., pp. 625-632, MIT Press, 1995.
  9. [9] M. Saroya, G. Best, and G. A. Hollinger, “Roadmap Learning for Probabilistic Occupancy Maps With Topology-Informed Growing Neural Gas,” IEEE Robotics and Automation Letters, Vol.6, No.3, pp. 4805-4812, 2021.
  10. [10] A. A. Saputra, W. H. Chin, Y. Toda, N. Takesue, and N. Kubota, “Dynamic density topological structure generation for real-time ladder affordance detection,” 2019 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS), pp. 3439-3444, 2019.
  11. [11] N. Mirehi, M. Tahmasbi, and A. T. Targhi, “Hand gesture recognition using topological features,” Multimedia Tools and Applications, Vol.78, No.10, pp. 13361-13386, 2019.
  12. [12] E. Ventocilla, R. M. Martins, F. Paulovich, and M. Riveiro, “Scaling the Growing Neural Gas for Visual Cluster Analysis,” Big Data Research, Vol.26, Article No.100254, 2021.
  13. [13] J. C. Bezdek, “A Convergence Theorem for the Fuzzy ISODATA Clustering Algorithms,” IEEE Trans. on Pattern Analysis and Machine Intelligence, Vol.PAMI-2, No.1, pp. 1-8, 1980.
  14. [14] R. J. Hathaway and C. B. James, “Recent convergence results for the fuzzy c-means clustering algorithms,” J. of Classification, Vol.5, pp. 237-247, 1988.
  15. [15] J. MacQueen, “Some methods for classification and analysis of multivariate observations,” Proc. of the 5th Berkeley Symp. on Mathematical Statistics and Probability, Volume 1, pp. 281-297, 1967.
  16. [16] J. Liang, L. Bai, C. Dang, and F. Cao, “The K-Means-Type Algorithms Versus Imbalanced Data Distributions,” IEEE Trans. on Fuzzy Systems, Vol.20, No.4, pp. 728,745, 2012.
  17. [17] K. Nigam, A. K. McCallum, S. Thrun, and T. Mitchell, “Text classification from labeled and unlabeled documents using EM,” Machine Learning, Vol.39, Issue 2-3, pp. 103-134, 2000.
  18. [18] S. Goldwater and G. Tom, “A fully Bayesian approach to unsupervised part-of-speech tagging,” Proc. of the 45th Annual Meeting of the Association of Computational Linguistics, Vol.45, No.1, pp. 744-751, 2007.
  19. [19] A. Baraldi and P. Blonda, “A survey of fuzzy clustering algorithms for pattern recognition. I,” IEEE Trans. on Systems, Man, and Cybernetics, Part B, Vol.29, No.6, pp. 778-785, 1999.
  20. [20] D. T. Anderson, J. C. Bezdek, M. Popescu, and J. M. Keller, “Comparing Fuzzy, Probabilistic, and Possibilistic Partitions,” IEEE Trans. on Fuzzy Systems, Vol.18, No.5, pp. 906-918, 2010.
  21. [21] D. Pelleg and A. W. Moore, “X-means: Extending K-means with Efficient Estimation of the Number of Clusters,” Proc. of the 17th Int. Conf. on Machine Learning (ICML’00), pp. 727-734, 2000.
  22. [22] B. Fritzke, “Growing cell structures – a self-organizing network for unsupervised and supervised learning,” Neural Networks, Vol.7, No.9, pp. 1441-1460, 1994.
  23. [23] F. Shen and O. Hasegawa, “An incremental network for on-line unsupervised classification and topology learning,” Neural Networks, Vol.19, No.1, pp. 90-106, 2006.
  24. [24] H. Zhang, X. Xiao, and O. Hasegawa, “A Load-Balancing Self-Organizing Incremental Neural Network,” IEEE Trans. on Neural Networks and Learning Systems, Vol.25, No.6, pp. 1096-1105, 2014.
  25. [25] A. Rauber, D. Merkl, and M. Dittenbach, “The growing hierarchical self-organizing map: exploratory analysis of high-dimensional data,” IEEE Trans. on Neural Networks, Vol.13, No.6, pp. 1331-1341, 2002.
  26. [26] A. Forti and G. L. Foresti, “Growing Hierarchical Tree SOM: An unsupervised neural network with dynamic topology,” Neural networks, Vol.19, No.10, pp. 1568-1580, 2006.
  27. [27] T. Kohonen, “Self-organizing maps,” Springer Series in Information Sciences book series, Vol.30, Springer Science & Business Media, 2001.
  28. [28] T. Martinetz and K. Schulten, “A ‘neural-gas’ network learns topologies,” Artificial Neural Networks: Proc. of the 1991 Int. Conf. on Artificial Neural Networks, pp. 397-402, 1991.
  29. [29] A. Baraldi and P. Blonda, “A survey of fuzzy clustering algorithms for pattern recognition. II,” IEEE Transactions on Systems, Man, and Cybernetics, Part B, Vol.29, No.6, pp. 786-801, 1999.
  30. [30] B. Fritzke, “A self-organizing network that can follow non-stationary distributions,” Artificial Neural Networks – Int. Conf. on Artificial Neural Networks (ICANN’97), pp. 613-618, 1997.
  31. [31] G. Karypis, E.-H. Han, and V. Kumar, “Chameleon: Hierarchical clustering using dynamic modeling,” Computer, Vol.32, No.8, pp. 68-75, 1999.
  32. [32] S. Fortunato, “Community detection in graphs,” Physics Reports, Vol.486, No.3-5, pp. 75-174, 2010.
  33. [33] R. Xu and D. Wunsch, “Survey of clustering algorithms,” IEEE Trans. on Neural Networks, Vol.16, No.3, pp. 645-678, 2005.
  34. [34] C. J. Veenman, M. J. T. Reinders, and E. Backer, “A maximum variance cluster algorithm,” IEEE Trans. on Pattern Analysis and Machine Intelligence, Vol.24, No.9, pp. 1273-1280, 2002.
  35. [35] H. Chang and D.-Y. Yeung, “Robust path-based spectral clustering,” Pattern Recognition, Vol.41, No.1, pp. 191-203, 2008.
  36. [36] A. Gionis, H. Mannila, and P. Tsaparas, “Clustering aggregation,” ACM Trans. on Knowledge Discovery from Data, Vol.1, No.1, Article 4, 2007.
  37. [37] E. Lopez-Rubio and E. J. Palomo, “Growing Hierarchical Probabilistic Self-Organizing Graphs,” IEEE Trans. on Neural Networks, Vol.22, No.7, pp. 997-1008, 2011.
  38. [38] T. Caliński and J. Harabasz, “A dendrite method for cluster analysis,” Communications in Statistics, Vol.3, No.1, pp. 1-27, 1974.
  39. [39] D. L. Davies and D. W. Bouldin, “A Cluster Separation Measure,” IEEE Trans. on Pattern Analysis and Machine Intelligence, Vol.PAMI-1, No.2, pp. 224-227, 1979.
  40. [40] A. Likas, N. Vlassis, and J. J. Verbeek, “The global k-means clustering algorithm,” Pattern Recognition, Vol.36, No.2, pp. 451-461, 2003.

Creative Commons License  This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.

*This site is desgined based on HTML5 and CSS3 for modern browsers, e.g. Chrome, Firefox, Safari, Edge, Opera.

Last updated on Apr. 18, 2024