Paper:
Ameliorated Frenet Trajectory Optimization Method Based on Artificial Emotion and Equilibrium Optimizer
Xiangdong Wu, Kaoru Hirota, Bijun Tang, Yaping Dai, and Zhiyang Jia†
School of Automation, Beijing Institute of Technology
No.5 Zhongguancun South Street, Haidian District, Beijing 100081, China
†Corresponding author
An ameliorated Frenet trajectory optimization (AFTO) method based on artificial emotion (AE) and an equilibrium optimizer (EO) is proposed for the local trajectory planning of an unmanned ground vehicle (UGV). An artificial emotional potential field (AEPF) model is established to simulate AE. To realize a humanoid driving mode with emotional intelligence, AE is introduced into the Frenet trajectory optimization (FTO) method to determine the optimal trajectory. Based on the optimal discrete goal state of the FTO method, a first-sampling-then-optimization (FSTO) framework combining the FTO method with the EO is designed to obtain the optimal trajectory in a continuous goal state space. With different AEPF levels corresponding to different types of obstacles, simulation results show that the AEPF effectively adjusts the trajectory into different levels of safe distance between the UGV and obstacles corresponding to the humanoid driving mode. From the results of 30 independent experiments based on the AEPF, the FSTO framework in the AFTO method is effective for optimizing the trajectory of the FTO method at a lower cost. Moreover, the effectiveness of the proposed method for different types of roads is verified on a straight road and a curved road with obstacles in simulation. The improvement based on emotional intelligence and trajectory optimization in the AFTO method provides a humanoid driving mode for the UGV in the continuous goal state space.
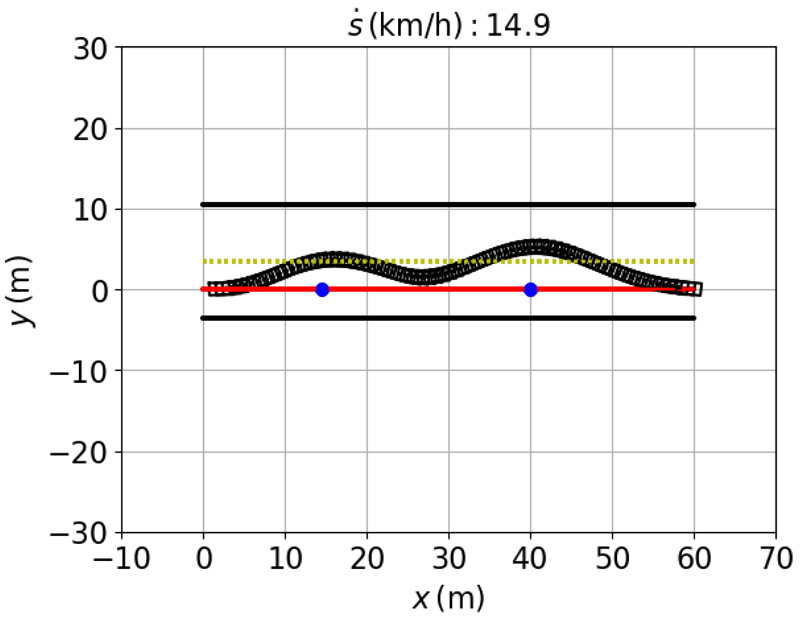
Trajectory of UGV for AFTO method
- [1] B. Paden, M. Cap, S. Z. Yong, D. Yershov, and E. Frazzoli, “A survey of motion planning and control techniques for self-driving urban vehicles,” IEEE Trans. on Intelligent Vehicles, Vol.1, No.1, pp. 33-55, 2016.
- [2] S. A. Goll, S. S. Luksha, V. S. Leushkin, and A. G. Borisov, “Unmanned ground vehicle local trajectory planning algorithm,” 2016 5th Mediterranean Conf. on Embedded Computing (MECO), pp. 317-321, 2016.
- [3] H. Wada, J. Kinugawa, and K. Kosuge, “Trajectory planning in time augmented C-space using RRT with sampling point including velocity determined by initial conditions,” 2020 IEEE/SICE Int. Symposium on System Integration (SII), pp. 170-175, 2020.
- [4] B. Li, Q. Kong, Y. Zhang, Z. Shao, Y. Wang, X. Peng, and D. Yan, “On-road trajectory planning with spatio-temporal RRT* and always-feasible quadratic program,” 2020 IEEE 16th Int. Conf. on Automation Science and Engineering (CASE), pp. 942-947, 2020.
- [5] J. Jahanpour, M. Motallebi, and M. Porghoveh, “A novel trajectory planning scheme for parallel machining robots enhanced with NURBS curves,” J. of Intelligent & Robotic Systems, Vol.82, No.2, pp. 257-275, 2016.
- [6] W. Chen, H. Fang, Y. Yang, and W. He, “Optimal trajectory planning for delta robot based on three-parameter Lame curve,” 2017 2nd Int. Conf. on Cybernetics, Robotics and Control (CRC), pp. 39-44, 2017.
- [7] D. Chen, S. Li, J. Wang, Y. Feng, and Y. Liu, “A multi-objective trajectory planning scheme for parallel assembly mechanism with B-spline curves,” 2018 IEEE 15th Int. Conf. on Networking, Sensing and Control (ICNSC), pp. 1-6, 2018.
- [8] L. Petrovic, J. Persic, M. Seder, and I. Markovic, “Stochastic optimization for trajectory planning with heteroscedastic Gaussian processes,” 2019 European Conf. on Mobile Robots (ECMR), pp. 1-6, 2019.
- [9] B. Li, Y. Zhang, F. Dou, and Y. Liu, “Real-time trajectory planning for AGV in the presence of moving obstacles: A first-search-then-optimization approach,” arXiv preprint arXiv:1902.06201, 2019.
- [10] H. Hu, Y. Wu, J. Xu, and Q. Sun, “Cuckoo search-based method for trajectory planning of quadrotor in an urban environment,” Proc. of the Institution of Mechanical Engineers, Part G: J. of Aerospace Engineering, Vol.233, No.12, pp. 4571-4582, 2019.
- [11] P. Sudhakara and V. Ganapathy, “Trajectory planning of a mobile robot using enhanced A-star algorithm,” Indian J. of Science and Technology, Vol.9, No.41, pp. 1-10, 2016.
- [12] Z. Boroujeni, D. Goehring, F. Ulbrich, D. Neumann, and R. Rojas, “Flexible unit A-star trajectory planning for autonomous vehicles on structured road maps,” 2017 IEEE Int. Conf. on Vehicular Electronics and Safety (ICVES), pp. 7-12, 2017.
- [13] Y. He, Q. Gao, D. Zhao, and W. Liu, “The trajectory planning of autonomous vehicle based on improved RRT algorithm,” J. of Northwest University (Natural Science Edition), Vol.48, No.5, pp. 651-658, 2018.
- [14] S. Williams, X. Wang, D. Angley, C. Gilliam, B. Moran, R. Ellem, T. Jackson, and A. Bessell, “Dynamic target driven trajectory planning using RRT,” 2019 22th Int. Conf. on Information Fusion, pp. 1-8, 2019.
- [15] X. Li, Z. Sun, D. Cao, D. Liu, and H. He, “Development of a new integrated local trajectory planning and tracking control framework for autonomous ground vehicles,” Mechanical Systems and Signal Processing, Vol.87, pp. 118-137, 2017.
- [16] D. Zeng, Z. Yu, P. Zhang, and H. Chen, “Cubic B-spline curve for obstacle avoidance trajectory planning of unmanned vehicle,” J. of Tongji University (NATURAL SCIENCE), Vol.47, No.S1, pp. 165-169, 2019.
- [17] B. Li, H. Liu, D. Xiao, G. Yu, and Y. Zhang, “Centralized and optimal motion planning for large-scale AGV systems: A generic approach,” Advances in Engineering Software, Vol.106, pp. 33-46, 2017.
- [18] B. Li and Z. Shao, “Precise trajectory optimization for articulated wheeled vehicles in cluttered environments,” Advances in Engineering Software, Vol.92, pp. 40-47, 2016.
- [19] M. Werling, J. Ziegler, S. Kammel, and S. Thrun, “Optimal trajectory generation for dynamic street scenarios in a Frenet frame,” 2010 IEEE Int. Conf. on Robotics and Automation, pp. 987-993, 2010.
- [20] J. S. Lerner, Y. Li, P. Valdesolo, and K. S. Kassam, “Emotion and decision making,” Annual Review of Psychology, Vol.66, pp. 799-823, 2015.
- [21] Y. Zhang and T. Chen, “A Q-learning algorithm applied to the behavioural decision-making of affective virtual human,” 2017 19th Int. Conf. on Advanced Communication Technology (ICACT), pp. 403-407, 2017.
- [22] Y. Maeda and S. Geshi, “Human-robot interaction using Markovian emotional model based on facial recognition,” 2018 Joint 10th Int. Conf. on Soft Computing and Intelligent Systems (SCIS) and 19th Int. Symposium on Advanced Intelligent Systems (ISIS), pp. 209-214, 2018.
- [23] A. Faramarzi, M. Heidarinejad, B. Stephens, and S. Mirjalili, “Equilibrium optimizer: A novel optimization algorithm,” Knowledge-Based Systems, Vol.191, p. 105190, 2020.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.