Paper:
Direct Policy Search Reinforcement Learning Based on Variational Bayesian Inference
Nobuhiko Yamaguchi
Graduate School of Science and Engineering, Faculty of Science and Engineering, Saga University
1 Honjo, Saga-shi, Saga 840-8502, Japan
Direct policy search is a promising reinforcement learning framework particularly for controlling continuous, high-dimensional systems. Peters et al. proposed reward-weighted regression (RWR) as a direct policy search. The RWR algorithm estimates the policy parameter based on the expectation-maximization (EM) algorithm and is therefore prone to overfitting. In this study, we focus on variational Bayesian inference to avoid overfitting and propose direct policy search reinforcement learning based on variational Bayesian inference (VBRL). The performance of the proposed VBRL is assessed in several experiments involving a mountain car and a ball batting task. These experiments demonstrate that VBRL yields a higher average return and outperforms the RWR.
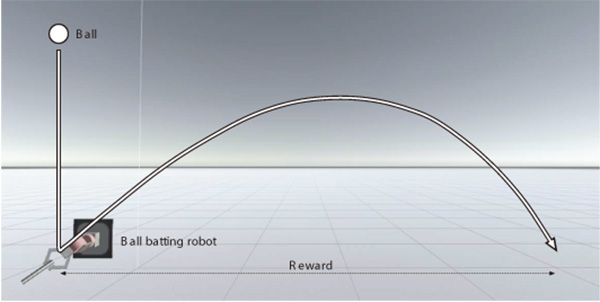
Ball batting task
- [1] R. J. Williams, “Simple Statistical Gradient-Following Algorithms for Connectionist Reinforcement Learning,” Machine Learning, Vol.8, pp. 229-256, 1992.
- [2] R. S. Sutton and A. G. Barto, ”Reinforcement Learning: An Introduction,” MIT Press, 1998.
- [3] P. Dayan and G. E. Hinton, “Using Expectation-Maximization for Reinforcement Learning,” Neural Computation, Vol.9, No.2, pp. 271-278, 1997.
- [4] J. Peters and S. Schaal, “Reinforcement Learning by Reward-Weighted Regression for Operational Space Control,” Proc. of the 24th Int. Conf. on Machine Learning (ICML 2007), pp. 745-750, 2007.
- [5] M. P. Deisenroth, G. Neumann, and J. Peters, “A Survey on Policy Search for Robotics,” Foundations and Trends in Robotics, Vol.2, Nos.1-2, pp. 388-403, 2013.
- [6] H. Attias, “Inferring parameters and structure of latent variable models by variational bayes,” Proc. of the 15th Conf. on Uncertainty in Artificial Intelligence, pp. 21-30, 1999.
- [7] M. J. Beal, “Variational Algorithms for Approximate Bayesian Inference,” Ph.D. thesis, Gatsby Computational Neuroscience Unit, University College London, 2003.
- [8] S. P. Singh and R. S. Sutton, “Reinforcement Learning with Replacing Eligibility Traces,” Machine Learning, Vol.22, Nos.1-3, pp. 123-158, 1996.
- [9] M. E. Taylor, G. Kuhlmann, and P. Stone, “Autonomous Transfer for Reinforcement Learning,” Proc. of the 7th Int. Joint Conf. on Autonomous Agents and Multiagent Systems, Vol.1, pp. 283-290, 2008.
- [10] A. Dempster, N. Laird, and D. Rubin, “Maximum Likelihood from Incomplete Data via the EM Algorithm,” J. of the Royal Statistical Society, Series B (Methodological), Vol.39, No.1, pp. 1-38, 1977.
- [11] R. M. Neal and G. E. Hinton, “A view of the EM algorithm that justifies incremental, sparse, and other variants,” M. I. Jordan (Ed.), “Learning in Graphical Models,” pp. 355-368, MIT Press, 1999.
- [12] M. Sato, “Online Model Selection Based on the Variational Bayes,” Neural Computation, Vol.13, No.7, pp. 1649-1681, 2001.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.