Paper:
Designation of Candidate Solutions in Differential Evolution Based on Bandit Algorithm and its Evaluation
Masaya Sakakibara, Akira Notsu, Seiki Ubukata, and Katsuhiro Honda
Osaka Prefecture University
1-1 Gakuen-cho, Nakaku, Sakai, Osaka 599-8531, Japan
We propose UCT-Grid Area Search (UCT-GAS), which is an efficient optimization method that roughly estimates specific values in areas, and consider exploration and exploitation in optimization problems. This approach divides the search space and imagines it to be a multi-armed bandit, which enables us to use bandit algorithms to solve mathematical programming problems. Although the search speed is fast than other search algorithm like differential evolution, it might converge to a local solution. In this study, we improve this algorithm by replacing its random search part with differential evolution after several searches. Comparative experiments confirmed the search ability of the optimal solution, and our method benefits by showing that it avoids falling into a local solution and that its search speed is fast.
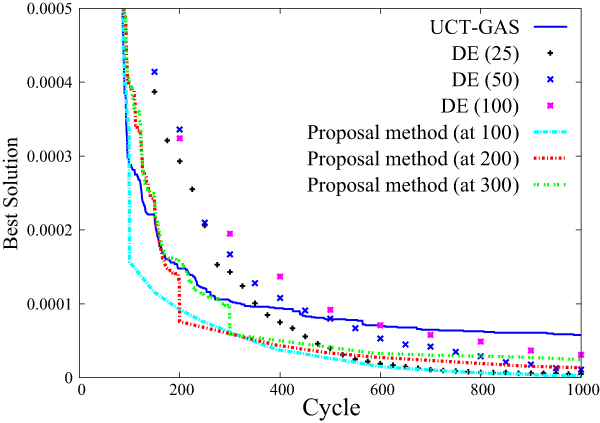
Result of DE initialized by UCT
- [1] J.-Y. Audibert, R. Munos, and C. Szepesvári, “Exploration-exploitation trade-off using variance estimates in multi-armed bandits,” Theoretical Computer Science, Vol.410, pp. 1876-1902, 2009.
- [2] A. Notsu, H. Kawakami, K. Honda, and S. Ubukata, “Development of general-purpose optimization methods based on bandit algorithm,” J. of Japan Society for Fuzzy Theory and Intelligent Informatics, Vol.28, No.1, pp. 522-534, 2016 (in Japanese).
- [3] R. Storn and K. Price, “Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces,” J. of global optimization, Vol.11, No.4, pp. 341-359, 1997.
- [4] M. Shibasaka, A. Hara, T. Ichimura, and T. Takahama, “Species-based differential evolution for multimodal function optimization,” IEICE Trans. on Information and Systems, Vol.J92-D, No.7, pp. 1003-1014, 2009 (in Japanese).
- [5] P. Auer, N. Cesa-Bianchi, and P. Fischer, “Finite-time analysis of the multi-armed bandit problem,” Machine Learning, Vol.47, No.2-3, pp. 235-256, 2002.
- [6] J.-Y. Audibert and S. Bubeck, “Regret bounds and minimax policies under partial monitoring,” J. of Machine Learning Research, Vol.11, pp. 2785-2836, 2010.
- [7] L. Kocsis and C. Szepesvari, “Discounted UCB,” 2nd PASCAL Challenges Workshop, 2006.
- [8] A. Garivier and O. Cappe, “The KL-UCB algorithm for bounded stochastic bandits and beyond,” S. M. Kakade and U. von Luxburg (Eds.), Proc. of the 24th Annual Conf. on Learning Theory (COLT 2011), pp. 359-376, 2011.
- [9] J. Honda and A. Takemura, “An asymptotically optimal bandit algorithm for bounded support models,” A. T. Kalai and M. Mohri (Eds.), Proc. of the 23rd Conf. on Learning Theory (COLT 2010), Omnipress, pp. 67-79, 2010.
- [10] L. Kocsis and C. Szepesvari, “Bandit-based Monte Carlo Planning,” Proc. of the 17th European Conf. on Machine Learning, Springer Berlin Heidelberg, 2006.
- [11] P. Auer, N. Cesa-Bianchi, Y. Freund, and R. E. Schapire, “Gambling in a rigged casino, the adversarial multi-armed bandit problem,” Proc. of the 36th Annual Symp. on Foundations of Computer Science, pp. 322-331, 1995.
- [12] H. Kato, “Zen, the world strongest computer Go player,” J. of the Japanese Society for Artificial Intelligence, Vol.27, No.5, pp. 501-504, 2012 (in Japanese).
- [13] A. Notsu, S. Kane, S. Ubukata, and K. Honda, “Application of the UCT algorithm for noisy optimization problems,” Proc. of Joint 8th Int. Conf. on Soft Computing and Intelligent Systems and 17th Int. Symp. on Advanced Intelligent Systems, pp. 48-53, 2016.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.