Paper:
Bifurcation Analysis and Impulsive Control of Genetic Regulatory Networks with Multi Delays
Feng Liu*,**,†, Jie Ren*, Ting Dong*, and Shiqi Zheng*,**
*School of Automation, China University of Geosciences
No. 388 Lumo Road, Hongshan District, Wuhan, Hubei 430074, China
**Hubei key Laboratory of Advanced Control and Intelligent Automation for Complex Systems
Wuhan, Hubei 430074, China
†Corresponding author
In this study, the stability and Hopf bifurcation of a genetic regulatory network with delays are addressed. Some bifurcations may cause network oscillation and induce instability. An impulsive control method is proposed to control the bifurcations. A numerical simulation was performed to demonstrate the effectiveness of the theoretical results.
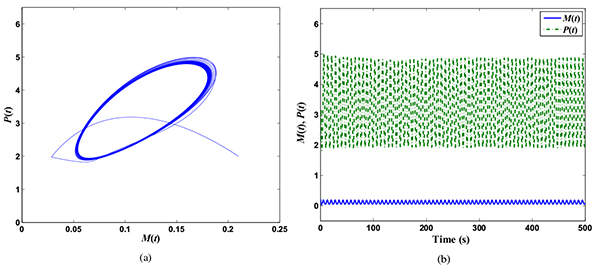
Bifurcation dynamics of gene networks
- [1] M. B. Elowitz and S. Leibler, “A synthetic oscillatory network of transcriptional regulators,” Nature, Vol.403, No.6767, pp. 335-338, 2000.
- [2] T. S. Gardner, C. R. Cantor, and J. J. Collins, “Construction of a genetic toggle switch in Escherichia coli,” Nature, Vol.403, No.6767, pp. 339-342, 2000.
- [3] A. Becskei and L. Serrano, “Engineering stability in gene networks by autoregulation,” Nature, Vol.405, No.6786, pp. 590-593, 2000.
- [4] L. Chen and K. Aihara, “Stability of genetic regulatory networks with time delay,” IEEE Trans. on Circuits and Systems I: Fundamental Theory Applications, Vol.49, Issue 5, pp. 602-608, 2002.
- [5] H. de Jong, “Modeling and Simulation of Genetic Regulatory Systems: A Literature Review,” J. Computational Biology, Vol.9, Issue 1, pp. 67-103, 2002.
- [6] T. Kobayashi, L. Chen, and K. Aihara, “Modeling Genetic Switches with Positive Feedback Loops,” J. Theoretical Biology, Vol.221, Issue 3, pp. 379-399, 2003.
- [7] D. W. Austin, M. S. Allen, et al., “Gene network shaping of inherent noise spectra,” Nature, Vol.439, No.7076, pp. 608-611, 2006.
- [8] C. Li, L. Chen, and K. Aihara, “Stability of Genetic Networks with SUM Regulatory Logic: Lur’e System and LMI Approach,” IEEE Trans. on Circuits and Systems I: Regular Papers, Vol.53, Issue 11, pp. 2451-2458, 2006.
- [9] J. Shen, Z. Liu, W. Zheng, F. Xu, and L. Chen, “Oscillatory dynamics in a simple gene regulatory network mediated by small RNAs,” Physica A: Statistical Mechanics and its Applications, Vol.388, Issue 14, pp. 2995-3000, 2009.
- [10] Z.-H. Guan and G. Chen, “On delayed impulsive Hopfield neural networks,” Neural Networks, Vol.12, Issue 2, pp. 273-280, 1999.
- [11] F. Liu, Z.-H. Guan, H. O. Wang, and Y. Li, “Impulsive control of bifurcations,” Mathematics and Computers in Simulation, Vol.79, Issue 7, pp. 2180-2191, 2009.
- [12] K. L. Cooke and Z. Grossman, “Discrete delay, distributed delay and stability switches,” J. of Mathematical Analysis and Applications, Vol.86, Issue 2, pp. 592-627, 1982.
- [13] B. D. Hassard, N. D. Kazarinoff, and Y.-H. Wan, “Theory and Application of Hopf Bifurcation,” Cambridge University Press, 1981.
- [14] J. K. Hale, “Theory of Functional Differential Equations,” Springer-Verlag, 1977.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.