Paper:
Intelligent Measurement of Spinal Curvature Using Cascade Gentle AdaBoost Classifier and Region-Based DRLSE
Liyuan Zhang, Jiashi Zhao†, Zhengang Jiang, and Huamin Yang
School of Computer Science and Technology, Changchun University of Science and Technology
No.7089 Weixing Road, Changchun 130022, China
†Corresponding author
For spinal curvature measurements, because of the anatomical complexity of the spine CT image, developing an automated method to avoid manual landmark is a challenging task. In this study, we propose an intelligent framework that integrates the cascade AdaBoost classifier and region-based distance regularized level set evolution (DRLSE) with the vertebral centroid measurement. First, the histogram-of-oriented-gradients based cascade gentle AdaBoost classifier is used to detect automatically and localize vertebral bodies from computer tomography (CT) spinal images. Considering these vertebral pathological images enables us to produce a diverse training dataset. Then, the DRLSE method introduces the local region information to converge the vertebral boundary quickly. The located bounding box is regarded as an accurate initial contour. This avoids the negative impact of manual initialization. Finally, we perform vertebral centroid extraction and spinal curve fitting. The spinal curvature angle is determined by calculating the angle between two tangents to the curve. We verified the effectiveness of the proposed method on 10 spine CT volumes. Quantitative comparison against the ground-truth centroids yielded a detection accuracy rate of 98.3% and a mean centroid location error of 1.15 mm. The comparative results with existing methods demonstrate that the proposed method can accurately detect and segment vertebral bodies. Furthermore, the spinal curvature can be automatically measured without manual landmark.
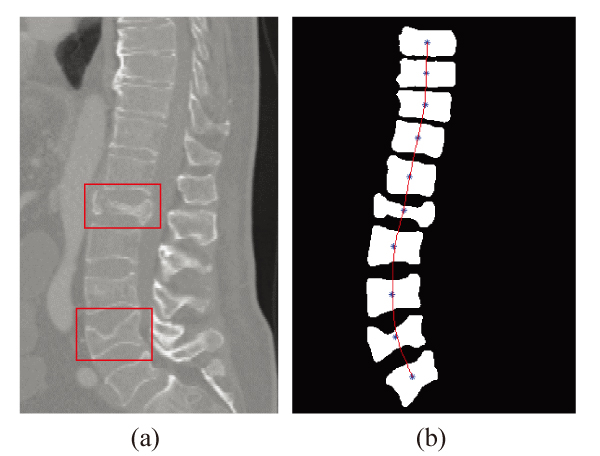
Spinal curvature measurement result
- [1] łabelcite:1 D. Forsberg, C. Lundström, M. Andersson, et al., “Model-based registration for assessment of spinal deformities in idiopathic scoliosis,” Physics in Medicine and Biology, Vol.59, No,2, pp. 311-328, 2013.
- [2] łabelcite:2 T. Vrtovec, F. Pernuš, and B. Likar, “A review of methods for quantitative evaluation of spinal curvature,” European Spine J., Vol.18, No.5, pp. 593-607, 2009.
- [3] łabelcite:3 M. Jiang, S. Zhang, H. Li, et al., “Computer-aided diagnosis of mammographic masses using scalable image retrieval,” IEEE Trans. on Biomedical Engineering, Vol.62, No.2, pp. 783-792, 2015.
- [4] łabelcite:4 B. Peralta and L. A. Caro, “Improved Object Recognition with Decision Trees Using Subspace Clustering,” J. Adv. Comput. Intell. Intell. Inform., Vol.20, No.1, pp. 41-48, 2016.
- [5] łabelcite:5 J. Barabáš, B. Babušiak, M. Gǎla, et al., “Computer-assisted analysis of spinal curvature parameters from CT images,” 35th IEEE Int. Conf. on Telecommunications and Signal Processing, pp. 574-577, 2012.
- [6] łabelcite:6 T. Vrtovec, B. Likar, and F. Pernus, “Manual and computerized measurement of coronal vertebral inclination on MRI images: A pilot study,” Clinical Radiology, Vol.68, No.8, pp. 807-814, 2013.
- [7] łabelcite:7 M. C. Tanure, A. P. Pinheiro, and A. S. Oliveira, “Reliability assessment of Cobb angle measurements using manual and digital methods,” The Spine J., Vol.10, No.9, pp. 769-774, 2010.
- [8] łabelcite:8 T. Illés and S. Somoskeöy, “Comparison of scoliosis measurements based on three-dimensional vertebra vectors and conventional two-dimensional measurements: advantages in evaluation of prognosis and surgical results,” European Spine J., Vol.22, No.6, pp. 1255-1263, 2013.
- [9] łabelcite:9 J.-Y. Hong, S.-W. Suh, H. N. Modi, et al., “Centroid method: an alternative method of determining coronal curvature in scoliosis. A comparative study versus Cobb method in the degenerative spine,” The Spine J., Vol.13, No.4, pp. 421-427, 2013.
- [10] łabelcite:10 H. Liao, A. Mesfin, and J. Luo, “Joint Vertebrae Identification and Localization in Spinal CT Images by Combining Short-and Long-Range Contextual Information,” IEEE Trans. on Medical Imaging, Vol.37, No.5, pp. 1266-1275, 2018.
- [11] łabelcite:11 D. Forsberg, E. Sjöblom, and J. L. Sunshine, “Detection and labeling of vertebrae in MR images using deep learning with clinical annotations as training data,” J. of Digital Imaging, Vol.30, No.4, pp. 406-412, 2017.
- [12] łabelcite:12 B. Glocker, D. Zikic, E. Konukoglu, D. R. Haynor, et al., “Vertebrae Localization in Pathological Spine CT via Dense Classification from Sparse Annotations,” Proc. of 16th Int. Conf. on Medical Image Computing and Computer-Assisted Intervention (MICCAI 2013), Part 2, pp. 262-270, 2013.
- [13] łabelcite:13 D. Zukić, A. Vlasák, J. Egger, et al., “Robust detection and segmentation for diagnosis of vertebral diseases using routine MR images,” Computer Graphics Forum, Vol.33, No.6, pp. 190-204, 2014.
- [14] łabelcite:14 B. M. Kelm, M. Wels, S. K. Zhou, et al., “Spine detection in CT and MR using iterated marginal space learning,” Med. Image Anal., Vol.17, No.8, pp. 1283-1292, 2013.
- [15] łabelcite:15 Y. L. Cai, L. Mark, T. L. David, et. al., “Multi-modal vertebrae recognition using Transformed Deep Convolution Network,” Computerized Medical Imaging and Graphics, Vol.51. pp. 11-19, 2016.
- [16] łabelcite:16 K. Zhang, H. Song, and L. Zhang, “Active contours driven by local image fitting energy,” Pattern Recognition, Vol.43, No.4, pp. 1199-1206, 2010.
- [17] łabelcite:17 S. Ghosh and V. Chaudhary, “Supervised methods for detection and segmentation of tissues in clinical lumbar MRI,” Computerized Medical Imaging and Graphics, Vol.38, No.7, pp. 639-649, 2014.
- [18] łabelcite:18 S. Kadoury, H. Labelle, and N. Paragios, “Spine segmentation in medical images using manifold embeddings and higher-order MRFs,” IEEE Trans. on Medical Imaging, Vol.32, No.7, pp. 1227-1238, 2013.
- [19] łabelcite:19 R. Korez, B. Ibragimov, B. Likar, et al., “A framework for automated spine and vertebrae interpolation-based detection and model-based segmentation,” IEEE Trans. on Medical Imaging, Vol.34, No.8, pp. 1649-1662, 2015.
- [20] łabelcite:20 S. Lankton and A. Tannenbaum, “Localizing Region-Based Active Contours,” IEEE Trans. Image Process., Vol.17, No.11, pp. 2029-2039, 2008.
- [21] łabelcite:21 C. Gan, W. Cao, M. Wu, et al., “Intelligent Nadaboost-ELM modeling method for formation drillability using well logging data,” J. Adv. Comput. Intell. Intell. Inform., Vol.20, No.7, pp. 1103-1111, 2016.
- [22] łabelcite:22 C. Li, C. Xu, C. Gui, et al., “Distance regularized level set evolution and its application to image segmentation,” IEEE Trans. Image Process., Vol.19, No.12, pp. 3243-3254, 2010.
- [23] łabelcite:23 Y. Xu, C. N. Li, X. L. Xu, et al., “A two-stage hog feature extraction processor embedded with SVM for pedestrian detection,” 2015 IEEE Int. Conf. on Image Processing (ICIP), pp. 3452-3455, 2015.
- [24] łabelcite:24 S. Yang, X. Liao, and U. K. Borasy, “A pedestrian detection method based on the HOG-LBP feature and Gentle AdaBoost,” Int. J. of Advancements in Computing Technology, Vol.4, No.19, pp. 553-560, 2012.
- [25] łabelcite:25 V. Magudeeswaran and J. F. Singh, “Contrast limited fuzzy adaptive histogram equalization for enhancement of brain images,” Int. J. of Imaging Systems and Technology, Vol.27, No.1, pp. 98-103, 2017.
- [26] łabelcite:26 F. Gibou, R. Fedkiw, and S. Osher, “A review of level-set methods and some recent applications,” J. of Computational Physics, Vol.355, pp. 82-109, 2017.
- [27] łabelcite:27 P. G. Guest, “Numerical methods of curve fitting,” Cambridge University Press, 2012.
- [28] łabelcite:28 R. Alonso, E. E. Jenkins, and A. V. Manohar, “A geometric formulation of Higgs effective field theory: measuring the curvature of scalar field space,” Physics Letters B, Vol.754, pp. 335-342, 2016.
- [29] łabelcite:29 The publicity spine CT database platform SpineWeb, http://spineweb.digitalimaginggroup.ca [accessed May 13, 2016]
- [30] łabelcite:30 S. Suo, N. Lin, H. Wang, et al., “Intravoxel incoherent motion diffusion weighted MR imaging of breast cancer at 3.0 tesla: comparison of different curve fitting methods,” J. of Magnetic Resonance Imaging, Vol.42, No.2, pp. 362-370, 2015.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.