Paper:
Crystalizing Effect of Simulated Annealing on Boltzmann Machine
Hiroki Shibata, Hiroshi Ishikawa, and Yasufumi Takama†
Graduate School of System Design, Tokyo Metropolitan University
6-6 Asahigaoka, Hino, Tokyo 191-0065, Japan
†Corresponding author
This paper proposes a method to estimate the posterior distribution of a Boltzmann machine. Due to high feature extraction ability, a Boltzmann machine is often used for both of supervised and unsupervised learning. It is expected to be suitable for multimodal data because of its bi-directional connection property. However, it needs a sampling method to estimate the posterior distribution, which becomes a problem during an inference period because of the computation time and instability. Therefore, it is usually converted to feedforward neural networks, which means to lose its bi-directional property. To deal with these problems, this paper proposes a method to estimate the posterior distribution of a Boltzmann machine fast and stably without converting it to feedforward neural networks. The key idea of the proposed method is to estimate the posterior distribution using a simulated annealing on non-uniform temperature distribution. The advantage of the proposed method against Gibbs sampling and conventional simulated annealing is shown through experiments with artificial dataset and MNIST. Furthermore, this paper also gives the mathematical analysis of Boltzmann machine’s behaviour with regard to temperature distribution.
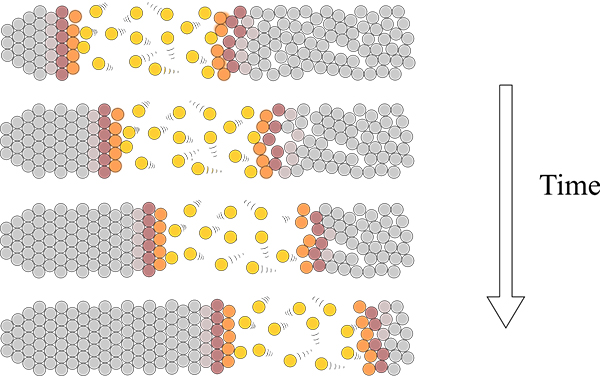
Crystallizing the distribution of BM
- [1] Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner, “Gradient-based learning applied to document recognition,” Proc. of The IEEE, Vol.86, No.11, pp. 2278-2324, 1998.
- [2] T. Mikolov, M. Karafiát, L. Burget, J. Cernoký, and S. Khudanpur, “Recurrent neural network based language model,” Proc. of Interspeech, 2010.
- [3] D. H. Ackley, et. al., “A learning algorithm for Boltzmann machines,” Cognitive Science, Vol.9, No.1, pp. 147-169, 1985.
- [4] R. Salakhutdinov and G. Hinton, “Deep Boltzmann machines,” Proc. of AI and Statistics, Vol.5, pp. 448-455, 2009.
- [5] N. T. Kuong, E. Uchino, and N. Suetake, “IVUS tissue characterization of coronary plaque by classification restricted Boltzmann machine,” J. Adv. Comput. Intell. Intell. Inform., Vol.21, No.1, pp. 67-73, 2017.
- [6] N. Srivastava and R. Salakhutdinov, “Multimodal learning with deep Boltzmann machines,” J. of Machine Learning Research, Vol.15, pp. 2949-2980, 2014.
- [7] S. Kirkpartrick, C. D. Gelatte, Jr., and M. P Vecchi, “Optimization by simulated annealing,” Science, Vol.220, No.4598, pp. 671-680, 1983.
- [8] G. E. Hinton and T. J. Sejnowski, “Optimal perceptual inference,” Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, pp. 448-453, 1983.
- [9] H. Shibata and Y. Takama, “Consideration on crystalizing simulated annealing for Boltzmann machine,” Proc. of 10th Int. Con. on Management of Digital EcoSystems, pp. 87-93, 2018.
- [10] H, Shibata and Y. Takama, “Index-based notation for random variable and probability space,” J. Adv. Comput. Intell. Intell. Inform., (accepted).
- [11] T. Tieleman, “Training restricted Boltzmann machines using approximations to the likelihood gradient,” Proc. of 25th Int. Conf. on Machine Learning, pp. 1064-1071, 2008.
- [12] N. Srivastava, et. al., “Dropout: A simple way to prevent neural networks from overfitting,” J. of Machine Learning Research, Vol.15, pp. 1929-1958, 2014.
- [13] C. M. Bishop, “Pattern recognition and machine learning,” Springer, corrected at 8th printing, 2006.
- [14] N. Metropolis, et al., “Equation of state calculations by fast computing machines,” The J. of Chemical Physics, Vol.21, No.6, pp. 1087-1092, 1953.
- [15] T. Kaiser and K. W. Benz, “Floating-zone growth of silicon in magnetic fields. III. Numerical Simulation,” J. of Crystal Growth, Vol.183, No.4, pp. 564-572, 1998.
- [16] A. A. Efros and T. K. Leung, “Texture synthesis by non-parametric sampling,” Proc. of the 7th IEEE Int. Conf. on Computer Vision, Vol.2, pp. 1033-1038, 1999.
- [17] X.-D. Liu, S. Osher and T. Chan, “Weighted essentially non-oscillatory schemes,” J. of Computational Physics, Vol.115, Issue 1, pp. 200-212, 1994.
- [18] M. Matsumoto and T. Nishimura, “Mersenne twister: A 623-dimensionally equidistributed uniform pseudo-random number generator,” ACM Trans. on Modeling and Computer Simulation (TOMACS), Vol.8, No.1, pp. 3-31, 1998.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.