Paper:
Humanoid Robot Motion Modeling Based on Time-Series Data Using Kernel PCA and Gaussian Process Dynamical Models
Jian Mi and Yasutake Takahashi
Department of Human and Artificial Intelligent Systems, Graduate School of Engineering, University of Fukui
3-9-1 Bunkyo, Fukui, Fukui 910-8507, Japan
In this article, contrary to popular studies on human motion learning, we focus on addressing the problem of humanoid robot motions directly. Performances of different kernel functions with principal components analysis (PCA) in Gaussian process dynamical models (GPDM) are investigated to build efficient humanoid robot motion models. A novel kernel-PCA-GPDM method is proposed for building different types of humanoid robot motion models. Compared with the standard-PCA-GPDM and auto-encoder-GPDM methods, our proposed method is more efficient in humanoid robot motion modeling. In this work, three types of NAO robot motion models are studied: walk-model, lateral-walk model, and wave-hand model, where motion data are collected from an Aldebaran NAO robot using magnetic rotary encoder sensors. Using kernel-PCA-GPDM method, the motion data are first projected from the high 23-dimension observation space to a 3-dimension low latent space. Then, three types of humanoid robot motion models are learned in the 3D latent space. Compared with other kernel-PCA-GPDM or auto-encoder-GPDM methods, our proposed novel kernel-PCA-GPDM method performs efficiently in motion learning. Finally, we realize humanoid robot motion representation to verify the motion models that we build. The experimental results show that our proposed kernel-PCA-GPDM method builds efficient and smooth motion models.
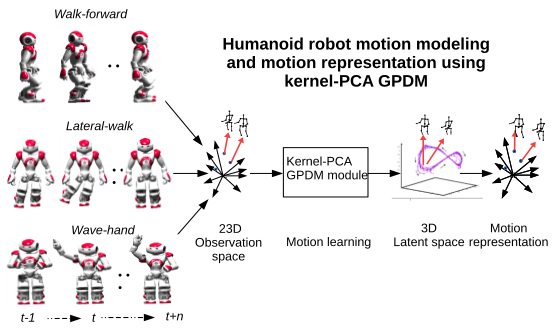
Three types of humanoid robot motion models are studied. Using kernel-PCA GPDM"," 3D motion models are built from 23-dimensional humanoid robot motion data. Then"," the learned 3D motion data are restored to verify the learned motion models
- [1] Y. Ou, J. Hu, Z. Wang, Y. Fu, X. Wu, and X. Li, “A Real-Time Human Imitation System Using Kinect,” Int. J. of Social Robotics, Vol.7, No.5, pp. 587-600, 2015.
- [2] S. Morante, J. G. Victores, A. Jardón, and C. Balaguer, “Humanoid robot imitation through continuous goal directed actions: an evolutionary approach,” Advanced Robotics, Vol.29, No.5, pp. 303-314, 2015.
- [3] J. Lei, M. Song, Z.-N. Li, and C. Chen, “Whole-body humanoid robot imitation with pose similarity evaluation,” Signal Processing, Vol.108, pp. 136-146, 2015.
- [4] W. He, W. Ge, Y. Li, Y. J. Liu, C. Yang, and C. Sun, “Model Identification and Control Design for a Humanoid Robot,” IEEE Trans. on Systems, Man, and Cybernetics: Systems, Vol.47, No.1, pp. 45-57, 2017.
- [5] P. Shahverdi and M. T. Masouleh, “A simple and fast geometric kinematic solution for imitation of human arms by a NAO humanoid robot,” 2016 4th Int. Conf. on Robotics and Mechatronics (ICROM), pp. 572-577, 2016.
- [6] J. M. Wang, D. J. Fleet, and A. Hertzmann, “Gaussian Process Dynamical Models for Human Motion,” IEEE Trans. on Pattern Analysis and Machine Intelligence, Vol.30, No.2, pp. 283-298, 2008.
- [7] N. Yamaguchi, “Visualizing State of Time-Series Data by Super-vised Gaussian Process Dynamical Models,” J. Adv. Comput. Intell. Intell. Inform., Vol.21, No.5, pp. 825-831, 2017.
- [8] T. Kim, J. Park, S. Heo, K. Sung, and J. Park, “Characterizing Dynamic Walking Patterns and Detecting Falls with Wearable Sensors Using Gaussian Process Methods,” Sensors, Vol.17, No.5, 2017.
- [9] Y. Kondo, S. Yamamoto, and Y. Takahashi, “Real-Time Posture Imitation of Biped Humanoid Robot Based on Particle Filter with Simple Joint Control for Standing Stabilization,” 2016 Joint 8th Int. Conf. on Soft Computing and Intelligent Systems (SCIS) and 17th Int. Symp. on Advanced Intelligent Systems (ISIS), pp. 130-135, 2016.
- [10] K. S. Hwang, W. C. Jiang, and Q. H. Yang, “Posture imitation and balance learning for humanoid robots,” 2016 Int. Conf. on Advanced Robotics and Intelligent Systems (ARIS), pp. 1-6, 2016.
- [11] Y. Takahashi, H. Hatano, Y. Maida, K. Usui, and Y. Meada, “Motion Segmentation and Recognition for Imitation Learning and Influence of Bias for Learning Walking Motion of Humanoid Robot Based on Human Demonstrated Motion,” J. Adv. Comput. Intell. Intell. Inform., Vol.19, No.4, 2015.
- [12] H. Kang and F. C. Park, “Humanoid motion optimization via nonlinear dimension reduction,” 2012 IEEE Int. Conf. on Robotics and Automation, pp. 1444-1449, 2012.
- [13] L. Raskin, M. Rudzsky, and E. Rivlin, “Dimensionality reduction using a Gaussian Process Annealed Particle Filter for tracking and classification of articulated body motions,” Computer Vision and Image Understanding, Vol.115, No.4, pp. 503-519, 2011.
- [14] R. Urtasun, D. J. Fleet, and P. Fua, “3D People Tracking with Gaussian Process Dynamical Models,” 2006 IEEE Computer Society Conf. on Computer Vision and Pattern Recognition (CVPR’06), Vol.1, pp. 238-245, 2006.
- [15] S. Sedai, M. Bennamoun, D. Q. Huynh, A. El-sallam, S. Foo, J. Alderson, and C. Lind, “3D human pose tracking using Gaussian process regression and particle filter applied to gait analysis of Parkinson’s disease patients,” 2013 IEEE 8th Conf. on Industrial Electronics and Applications (ICIEA), pp. 1636-1642, 2013.
- [16] N. D. Lawrence, “Gaussian Process Latent Variable Models for Visualisation of High Dimensional Data,” S. Thrun, L. K. Saul, and B. Schölkopf (eds.), Advances in Neural Information Processing Systems Vol.16, pp. 329-336. MIT Press, 2004.
- [17] J. Mi and Y. Takahashi, “Motion representation for humanoid robot based on Gaussian Process Dynamical models,” The 5th Int. Workshops on Advanced Computational Intelligence and Intelligent Informatics (IWACIII2017), 2017.
- [18] B. Schölkopf and A. J. Smola, “Learning with Kernels,” The MIT Press, 2001.
- [19] I. Rodriguez, A. Aguado, O. Parra, E. Lazkano, and B. Sierra, “NAO Robot as Rehabilitation Assistant in a Kinect Controlled System,” pp. 419-423, Springer Int. Publishing, Cham, 2017.
- [20] C. Li and X. Wang, “Visual localization and object tracking for the NAO robot in dynamic environment,” 2016 IEEE Int. Conf. on Information and Automation (ICIA), pp. 1044-1049, 2016.
- [21] Z. B. Wang, L. Yang, Z. P. Huang, J. K. Wu, Z. Q. Zhang, and L. X. Sun, “Human motion tracking based on complementary Kalman filter,” 2017 IEEE 14th Int. Conf. on Wearable and Implantable Body Sensor Networks (BSN), pp. 55-58, 2017.
- [22] Y. Deng, T. Mao, M. Shi, and Z. Wang, “Cloth Deformation Prediction Based on Human Motion,” 2016 Int. Conf. on Virtual Reality and Visualization (ICVRV), pp. 258-263, 2016.
- [23] B. Jokanovic, M. Amin, and B. Erol, “Multiple joint-variable do-mains recognition of human motion,” 2017 IEEE Radar Conf. (RadarConf), pp. 0948-0952, 2017.
- [24] H. Zhu, Y. Yu, Y. Zhou, and S. Du, “Dynamic Human Body Modeling Using a Single RGB Camera,” Sensors, Vol.16, 2016.
- [25] J. Bütepage, M. J. Black, D. Kragic, and H. Kjellström, “Deeprepresentation learning for human motion prediction and classification,” CoRR, abs/1702.07486, 2017.
- [26] F. Hu, W. Liu, X. Wu, and D. Luo, “Learning basic unit movementswith gate-model auto-encoder for humanoid arm motion control,” 2016 IEEE Int. Conf. on Information and Automation (ICIA), pp. 246-251, 2016.
- [27] P. Xu, M. Ye, Q. Liu, X. Li, L. Pei, and J. Ding, “Motion detection via a couple of auto-encoder networks,” 2014 IEEE Int. Conf. on Multimedia and Expo (ICME), pp. 1-6, 2014.
- [28] R. Urtasun, D. J. Fleet, and P. Fua, “3D People Tracking with Gaussian Process Dynamical Models,” 2006 IEEE Computer Society Conf. on Computer Vision and Pattern Recognition (CVPR’06), Vol.1, pp. 238-245, 2006.
- [29] N. Yamaguchi, “Visualizing States of Time-Series Data by Autoregressive Gaussian Process Dynamical Models,” J. Adv. Comput. Intell. Intell. Inform., Vol.21, No.5, 2017.
- [30] I. T. Jolliffe, “Principal Component Analysis,” Springer New York, 2002.
- [31] J. Su, D. Yi, C. Liu, L. Guo, and W.-H. Chen, “Dimension Reduction Aided Hyperspectral Image Classification with a Small-sized Training Dataset: Experimental Comparisons,” Sensors, Vol.17, No.12, 2017.
- [32] R. M. Neal, “Bayesian Learning for Neural Networks,” Springer New York, 1996.
- [33] D. J. Mackay, “Information Theory, Inference, and Learning Algorithms,” Cambridge University Press, 2003.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.