Paper:
Noise Reduction with Inference Based on Fuzzy Rule Interpolation at an Infinite Number of Activating Points: Toward Fuzzy Rule Learning in a Unified Inference Platform
Kiyohiko Uehara* and Kaoru Hirota**
*Ibaraki University
4-12-1 Nakanarusawa-cho, Hitachi, Ibaraki 316-8511, Japan
**Beijing Institute of Technology
5 South Zhongguancun Street, Haidian District, Beijing 100081, China
In order to provide a unified platform for fuzzy inference and fuzzy rule learning with noise-corrupted data, a method is proposed for reducing noise in learning data on the basis of a fuzzy inference method called α-GEMINAS (α-level-set and generalized-mean-based inference with fuzzy rule interpolation at an infinite number of activating points). It is expected to prevent fuzzy rules from overfitting to noise in learning data, especially when there is less learning data available for fuzzy rule optimization. The proposed method is named α-GEMI-ES (α-GEMINAS-based local-evolution toward slight linearity for global smoothness) in this paper. α-GEMI-ES iteratively performs α-GEMINAS and reduces the noise in each iteration. This paper mathematically proves that α-GEMI-ES effectively reduces the noise. The noise-reduction process is decisive and thus relies less on trial-and-error-based progress. The noise is reduced by a large amount in the early iterations and the amount of its reduction is decelerated in the later iterations where the deviation in the learning data is suppressed to a great extent. This property makes it easy to determine the termination conditions for the iterative process. Simulation results demonstrate that α-GEMI-ES properly reduces noise as the mathematical proof suggests. The above-mentioned properties indicate that α-GEMI-ES is feasible in practice for the unified platform.
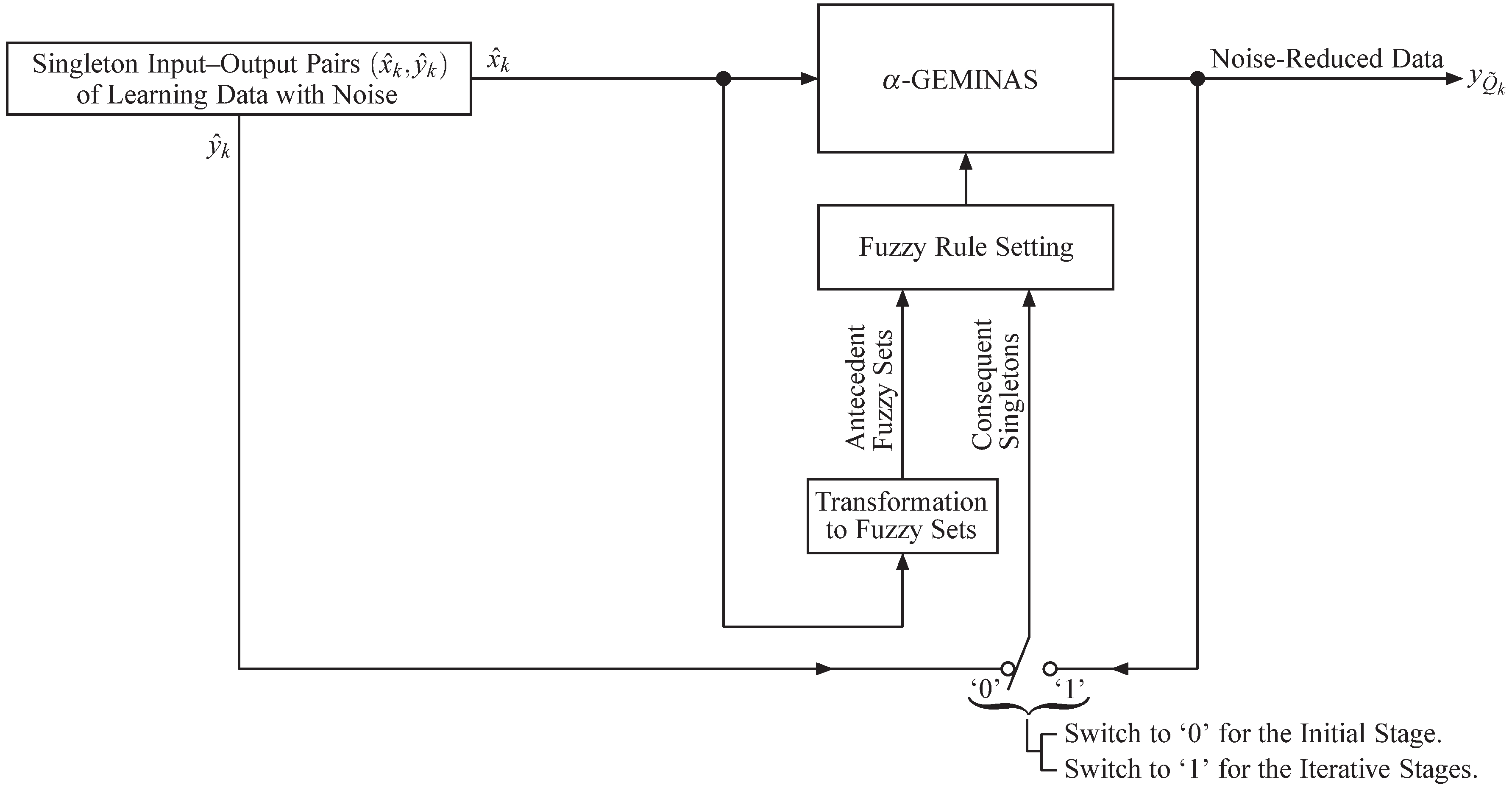
Process of noise reduction in α-GEMI-ES
- [1] L. A. Zadeh, “Outline of a new approach to the analysis of complex systems and decision processes,” IEEE Trans. Syst. Man Cybern., Vol.SMC-3, No.1, pp. 28-44, 1973.
- [2] L. T. Kóczy and K. Hirota, “Approximate reasoning by linear rule interpolation and general approximation,” Int. J. Approx. Reason., Vol.9, pp. 197-225, 1993.
- [3] L. T. Kóczy and K. Hirota, “Size reduction by interpolation in fuzzy rule bases,” IEEE Trans. Syst., Man, Cybern. B, Cybern., Vol.27, No.1, pp. 14-33, 1997.
- [4] D. Tikk and P. Baranyi, “Comprehensive analysis of a new fuzzy rule interpolation method,” IEEE Trans. Fuzzy Syst., Vol.8, No.3, pp. 281-296, 2000.
- [5] P. Baranyi, L. T. Kóczy, and T. D. Gedeon, “A generalized concept for fuzzy rule interpolation,” IEEE Trans. Fuzzy Syst., Vol.12, No.6, pp. 820-837, 2004.
- [6] K. W. Wong, D. Tikk, T. D. Gedeon, and L. T. Kóczy, “Fuzzy rule interpolation for multidimensional input spaces with applications: A case study,” IEEE Trans. Fuzzy Syst., Vol.13, No.6, pp. 809-819, 2005.
- [7] Z. Huang and Q. Shen, “Fuzzy interpolative reasoning via scale and move transformation,” IEEE Trans. Fuzzy Syst., Vol.14, No.2, pp. 340-359, 2006.
- [8] Z. Huang and Q. Shen, “Fuzzy interpolation and extrapolation: A practical approach,” IEEE Trans. Fuzzy Syst., Vol.16, No.1, pp. 13–28, 2008.
- [9] L. T. Kóczy and S. Kovács, “On the preservation of convexity and piecewise linearity in linear fuzzy rule interpolation,” Technical Report, LIFE Chair of Fuzzy Theory, DSS, Tokyo Institute of Technology, Japan, p. 23, 1993.
- [10] L. T. Kóczy and S. Kovács, “Shape of the fuzzy conclusion generated by linear interpolation of trapezoidal if ... then rules,” Fuzzy Set Theory and its Applications, Tatra Mountains Mathematical Publications, Mathematical Institute Slovak Academy of Science, Vol.6, pp. 83-93, Bratislava, Slovakia, 1995.
- [11] D. Tikk, Z. C. Johanyák, S. Kovács, and K. W. Wong, “Fuzzy rule interpolation and extrapolation techniques: criteria and evaluation guidelines,” J. Adv. Comput. Intell. Intell. Inform., Vol.15, No.3, pp. 254-263, 2011.
- [12] Q. Shen and L. Yang, “Generalization of scale and move transformation-based fuzzy interpolation,” J. Adv. Comput. Intell. Intell. Inform., Vol.15, No.3, pp. 288-298, 2011.
- [13] L. Kovács, “Compound distance function for similarity measurement between fuzzy sets,” J. Adv. Comput. Intell. Intell. Inform., Vol.15, No.3, pp. 299-303, 2011.
- [14] S. Kato and K. W. Wong, “Intelligent automated guided vehicle controller with reverse strategy,” J. Adv. Comput. Intell. Intell. Inform., Vol.15, No.3, pp. 304-312, 2011.
- [15] D. Vincze and S. Kovács, “Performance optimization of the fuzzy rule interpolation method ‘FIVE’,” J. Adv. Comput. Intell. Intell. Inform., Vol.15, No.3, pp. 313-320, 2011.
- [16] S. Jin, R. Diao, C. Quek, and Q. Shen, “Backward fuzzy rule interpolation,” IEEE Trans. Fuzzy Syst., Vol.22, No.6, pp. 1682-1698, 2014.
- [17] K. Uehara and K. Hirota, “Inference with fuzzy rule interpolation at an infinite number of activating points,” J. Adv. Comput. Intell. Intell. Inform., Vol.19, No.1, pp. 74-90, 2015.
- [18] S.-M. Chen and Z.-J. Chen, “Weighted fuzzy interpolative reasoning for sparse fuzzy rule-based systems based on piecewise fuzzy entropies of fuzzy sets,” Information Sciences, Vol.329, pp. 503-523, 2016.
- [19] C. Chen, N. M. Parthaláin, Y. Li, C. Price, C. Quek, and Q. Shen, “Rough-fuzzy rule interpolation,” Information Sciences, Vol.351, pp.1-17, 2016.
- [20] Y. Tan, J. Li, M. Wonders, F. Chao, H. P. H. Shum, and L. Yang, “Towards sparse rule base generation for fuzzy rule interpolation,” Proc. of 2016 IEEE Int. Conf. on Fuzzy Systems (FUZZ-IEEE 2016), Vancouver, Canada, pp. 110-117, 2016.
- [21] D. Vincze, “Fuzzy rule interpolation and reinforcement learning,” Proc. of 2017 IEEE 15th Int. Symp. on Applied Machine Intelligence and Informatics (SAMI 2017), Herl’any, Slovakia, pp. 173-178, 2017.
- [22] L. Yang, F. Chao, and Q. Shen, “Generalized adaptive fuzzy rule interpolation,”IEEE Trans. Fuzzy Syst., Vol.25, No.4, pp. 839-853, 2017.
- [23] K. Uehara and K. Hirota, “Multi-level control of fuzzy-constraint propagation in inference with fuzzy rule interpolation at an infinite number of activating points,” J. Adv. Comput. Intell. Intell. Inform., Vol.21, No.3, pp. 425-447, 2017.
- [24] K. Uehara and K. Hirota, “Noise reduction with inference based on fuzzy rule interpolation at an infinite number of activating points: A feasibility study,” Proc. of the 5th Int. Workshop on Advanced Computational Intelligence and Intelligent Informatics (IWACIII 2017), Beijing, China, AS3-1-2, pp. 1-8, 2017.
- [25] K. Uehara, T. Koyama, and K. Hirota, “Fuzzy inference with schemes for guaranteeing convexity and symmetricity in consequences based on α-cuts,” J. Adv. Comput. Intell. Intell. Inform., Vol.13, No.2, pp. 135-149, 2009.
- [26] K. Uehara, T. Koyama, and K. Hirota, “Inference with governing schemes for propagation of fuzzy convex constraints based on α-cuts,” J. Adv. Comput. Intell. Intell. Inform., Vol.13, No.3, pp. 321-330, 2009.
- [27] A. Kaufmann, “Introduction to the theory of fuzzy subsets,” New York: Academic Press, Vol.1, pp. 8-30, 1975.
- [28] N. R. Pal and J. C. Bezdek, “Measuring fuzzy uncertainty,” IEEE Trans. Fuzzy Syst., Vol.2, No.2, pp. 107-118, 1994.
- [29] R. R. Yager, “On the specificity of a possibility distribution,” Fuzzy Sets Syst., Vol.50, pp. 279-292, 1992.
- [30] R. R. Yager, “Measuring tranquility and anxiety in decision making: An application of fuzzy sets,” Int. J. General Systems, Vol.8, pp. 139-146, 1982.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.