Paper:
Conditional Distribution Prediction of Stock Returns and its Application on Risk Aversion Analysis
Yanyun Yao*,** and Bing Xu*
*Research Institute of Economic Statistics and Quantitative Economics, Zhejiang Gongshang University
18 Xuezheng Road, Xiasha University Town, Hangzhou 310018, China
**Department of Mathematics, Shaoxing University
900 Chengnan Avenue, Yuecheng District, Shaoxing 312000, China
Distribution prediction provides a complete description of forecasting uncertainty, which is of great significance to risk management. In this paper, the parametric method based on GARCH and the nonparametric method based on EWMA are both employed to model the conditional distributions of the SHCI and SZCI returns in Chinese stock market. As a result, the nonparametric method is better from the perspective of quantile evaluation. Furthermore, a simulated trading strategy based on time-varying quantiles is designed to analyze the trading yields of different levels of risk aversion. For the whole sample, compared with the buy-and-hold, SHCI has a higher profit in lower risk aversion and SZCI has higher profit only in a very narrow range when compared with the buy-and-hold strategy. In addition, the impact of IF:CSI 300 is considered. For the sub sample, before the emergence of IF:CSI 300, only a few investors with high risk aversion are able to achieve higher earnings from SHCI and there is hardly any opportunity for higher profit from SZCI. However, for the sub sample after the emergence of IF:CSI 300, many risk lovers and risk neutral investors have the opportunity to gain more profit than under the buy-and-hold strategy, both for SHCI and SZCI. The aforementioned conclusions imply that IF:CSI 300 may enhance Chinese stock market activity and liquidity and create more opportunities for investors who are not risk averse.
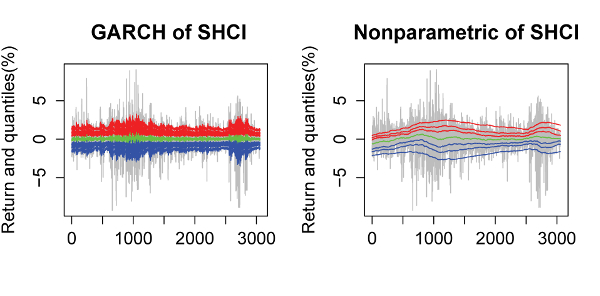
Quantiles of conditional distribution
- [1] P. Zhang, “A study on the correlation between China’s stock market and macro-economy,” Party School of CPC Central Committee, Doctoral Dissertation, 2013.
- [2] Y. Hong, “Some Recent Development in Financial Econometric,” China Economic Quartierly, Vol.1, No.2, pp. 249-268, 2002.
- [3] D. Massacci, “Predicting the distribution of stock returns: model formulation, statistical evaluation, VaR analysis and economic significance,” J. of Forecasting, Vol.34, pp. 191-208, 2015.
- [4] L. Li, S. Zhai, and M. Guan, “The time-varying of distribution about security market return rate and China’s related empirical data: an economic analysis,” Statistical Research, Vol.11, pp. 66-78, 2011.
- [5] T. Bollerslev, “Generalized autoregressive conditional heteroskedasticity,” J. of Econometrics, Vol.31, pp. 307-327, 1986.
- [6] A. Harvey and V. Oryshchenko, “Kernel density estimation for time series data,” Int. J. of Forecasting, Vol.28, pp. 3-14, 2012.
- [7] A. Pérez, “Comments on ‘Kernel density estimation for time series data’,” Int. J. of Forecasting, Vol.28, pp. 15-19, 2012.
- [8] T. Liu, N. Qiu, and W. Gu, “A Stock trading strategy based on time-Varying quantile theory,” J. Adv. Comput. Intell. Intell. Inform., Vol.19, No.3, pp. 417-422, 2015.
- [9] F. X. Diebold, T. A. Gunther, and A. S. Tay, “Evaluating density forecasts with applications to financial risk management,” Int. Economic Review, Vol.39, pp. 863-883, 1998.
- [10] Y. Hong and H. Li, “Nonparametric specification testing for continuous-time models with applications to term structure of interest rates,” Review of Financial Studies, Vol.18, pp. 37-84, 2005.
- [11] Y. Hong, H. Li, and F. Zhao, “Can the random walk model be beaten in out-ofsample density forecasts? Evidence from intraday foreign exchange rates,” J. of Econometrics, Vol.141, pp. 736-776, 2007.
- [12] G. González-Rivera and Y. Sun, “Density forecast evaluation in unstable environments,” Int. J. of Forecasting, Vol.33, pp. 416-432, 2017.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.