Top > JACIII > Adaptive Horizon Model Predictive Control with Equivalent-Inpu ...

single-jc.php

JACIII Vol.30 No.1 pp. 176-183
doi: 10.20965/jaciii.2026.p0176
(2026)

Research Paper:

Views over last 60 days: 27

Adaptive Horizon Model Predictive Control with Equivalent-Input-Disturbance for Vibration Suppression

Ruoyu Jiang*1,*2,*3 ORCID Icon, Xiang Yin*4 ORCID Icon, Seiichi Kawata*1,*2,*3 ORCID Icon, and Jinhua She*5,† ORCID Icon

*1School of Automation, China University of Geosciences
No.388 Lumo Road, Hongshan District, Wuhan, Hubei 430074, China

*2Hubei Key Laboratory of Advanced Control and Intelligent Automation for Complex Systems
No.388 Lumo Road, Hongshan District, Wuhan, Hubei 430074, China

*3Engineering Research Center of Intelligent Technology for Geo-Exploration, Ministry of Education
No.388 Lumo Road, Hongshan District, Wuhan, Hubei 430074, China

*4School of Electrical and Control Engineering, North China University of Technology
No.5 Jinyuanzhuang Road, Shijingshan District, Beijing 100144, China

*5School of Engineering, Tokyo University of Technology
1404-1 Katakuramachi, Hachioji, Tokyo 192-0982, Japan

†Corresponding author

Received:
January 15, 2025
Accepted:
August 29, 2025
Published:
January 20, 2026
Creative Commons License
Keywords:
vibration suppression, model-predictive control, adaptive horizon, equivalent-input-disturbance
Abstract

This paper presents a vibration suppression method for two-inertia mechanical transmission systems, combining adaptive horizon model predictive control (AHMPC) with the equivalent-input-disturbance (EID) approach. First, conventional model predictive control (MPC) is extended to an adaptive horizon formulation to reduce computational cost while effectively attenuating vibrations. Second, a quadratic-programming-based method is designed to efficiently solve the AHMPC optimization problem. Third, the EID approach is integrated to compensate for external disturbances. Finally, simulation studies on a two-inertia system demonstrate the effectiveness of the proposed method in achieving significant vibration suppression.

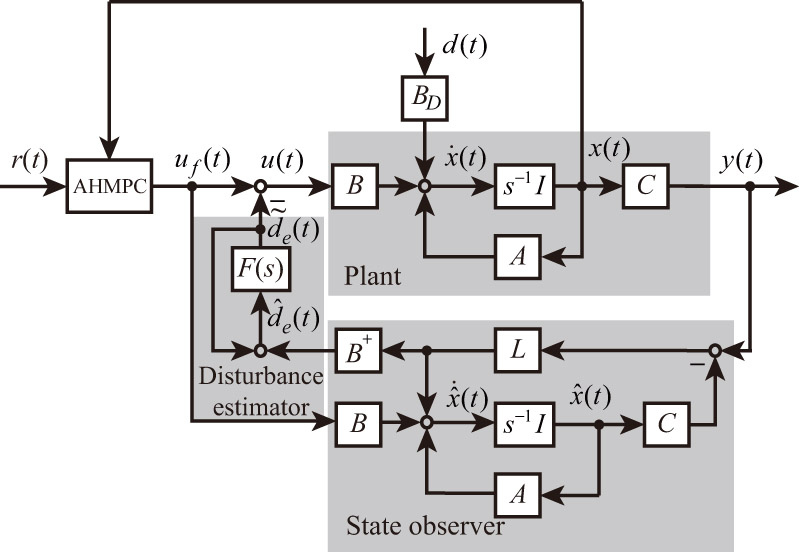
System configuration

System configuration

Cite this article as:
R. Jiang, X. Yin, S. Kawata, and J. She, “Adaptive Horizon Model Predictive Control with Equivalent-Input-Disturbance for Vibration Suppression,” J. Adv. Comput. Intell. Intell. Inform., Vol.30 No.1, pp. 176-183, 2026.
Data files:
References
  1. [1] H. Sheng, M.-X. He, J. Zhao, C. T. Kam, Q. Ding, and H. P. Lee, “The ABH-based lattice structure for load bearing and vibration suppression,” Int. J. of Mechanical Sciences, Vol.252, Article No.108378, 2023. https://doi.org/10.1016/j.ijmecsci.2023.108378
  2. [2] Y. Jin, X.-Y. Jia, Q.-Q. Wu, G.-C. Yu, X.-L. Zhang, S. Chen, and L.-Z. Wu, “Design of cylindrical honeycomb sandwich meta-structures for vibration suppression,” Mechanical Systems and Signal Processing, Vol.163, Article No.108075, 2022. https://doi.org/10.1016/j.ymssp.2021.108075
  3. [3] W. Wang, C. Hu, K. Zhou, and Z. Wang, “Time parameter mapping and contour error precompensation for multiaxis input shaping,” IEEE Trans. on Industrial Informatics, Vol.19, No.3, pp. 2640-2651, 2022. https://doi.org/10.1109/TII.2022.3158960
  4. [4] H. Yu, X. Liu, G.-P. Cai, X.-B. Zhou, and D. Du, “Active vibration control of a large space telescope based on H∞ control with unilateral and constrained input,” J. of the Franklin Institute, Vol.361, No.12, Article No.107029, 2024. https://doi.org/10.1016/j.jfranklin.2024.107029
  5. [5] X. Zhou, H. Wang, and Y. Tian, “Adaptive boundary iterative learning vibration control using disturbance observers for a rigid–flexible manipulator system with distributed disturbances and input constraints,” J. of Vibration and Control, Vol.28, Nos.11-12, pp. 1324-1340, 2022. https://doi.org/10.1177/1077546321990151
  6. [6] X. Jin, J. Wang, Z. Yan, L. Xu, G. Yin, and N. Chen, “Robust vibration control for active suspension system of in-wheel-motor-driven electric vehicle via μ-synthesis methodology,” J. of Dynamic Systems, Measurement, and Control, Vol.144, No.5, Article No.051007, 2022. https://doi.org/10.1115/1.4053661
  7. [7] P. Boscariol, D. Richiedei, and I. Tamellin, “Residual vibration suppression in uncertain systems: A robust structural modification approach to trajectory planning,” Robotics and Computer-Integrated Manufacturing, Vol.74, Article No.102282, 2022. https://doi.org/10.1016/j.rcim.2021.102282
  8. [8] Q. Li, Q. Xu, and R. Wu, “Low-frequency vibration suppression control in a two-mass system by using a torque feed-forward and disturbance torque observer,” J. of Power Electronics, Vol.16, No.1, pp. 249-258, 2016. https://doi.org/10.6113/JPE.2016.16.1.249
  9. [9] J. Rodriguez, M. Collet, and S. Chesné, “Active vibration control on a smart composite structure using modal-shaped sliding mode control,” J. of Vibration and Acoustics, Vol.144, No.2, Article No.021013, 2022. https://doi.org/10.1115/1.4053358
  10. [10] T. Yamada, R. Inada, and K. Ito, “Designing a model predictive controller for displacement control of axial piston pump,” Int. J. Automation Technol., Vol.18, No.1, pp. 113-127, 2024. https://doi.org/10.20965/ijat.2024.p0113
  11. [11] D. Zhang, M. Wu, C. Lu, L. Chen, W. Cao, and J. Hu, “Intelligent compensating method for MPC-based deviation correction with stratum uncertainty in vertical drilling process,” J. Adv. Comput. Intell. Intell. Inform., Vol.25, No.1, pp. 23-30, 2021. https://doi.org/10.20965/jaciii.2021.p0023
  12. [12] Z. Xie, S. Li, P. K. Wong, W. Li, and J. Zhao, “An improved gain-scheduling robust MPC for path following of autonomous independent-drive electric vehicles with time-varying and uncertainties,” Vehicle System Dynamics, Vol.63, No.4, pp. 695-721, 2025. https://doi.org/10.1080/00423114.2024.2351574
  13. [13] T. Chen, W. Yang, Z. Zhang, and X. Luo, “An efficient industrial robot calibrator with multiplaner constraints,” IEEE Trans. on Industrial Informatics, Vol.20, No.12, pp. 14341-14350, 2024. https://doi.org/10.1109/TII.2024.3450112
  14. [14] J. Peng, S. Cheng, and W. Liu, “Temperature control of cement rotary kiln sintering zone based on FCS-MPC with soft constraint of generalized triangular interval,” J. Adv. Comput. Intell. Intell. Inform., Vol.28, No.2, pp. 324-332, 2024. https://doi.org/10.20965/jaciii.2024.p0324
  15. [15] H. Xie, L. Dai, Y. Lu, and Y. Xia, “Disturbance rejection MPC framework for input-affine nonlinear systems,” IEEE Trans. on Automatic Control, Vol.67, No.12, pp. 6595-6610, 2021. https://doi.org/10.1109/TAC.2021.3133376
  16. [16] M. Schwenzer, M. Ay, T. Bergs, and D. Abel, “Review on model predictive control: An engineering perspective,” The Int. J. of Advanced Manufacturing Technology, Vol.117, No.5, pp. 1327-1349, 2021. https://doi.org/10.1007/s00170-021-07682-3
  17. [17] J. Morrison, R. Nagamune, and V. Grebenyuk, “An iterative learning approach to economic model predictive control for an integrated solar thermal system,” IFAC-PapersOnLine, Vol.53, No.2, pp. 12777-12782, 2020. https://doi.org/10.1016/j.ifacol.2020.12.1930
  18. [18] D. Yan, W. Zhang, H. Chen, and J. Shi, “Robust control strategy for multi-uavs system using MPC combined with Kalman-consensus filter and disturbance observer,” ISA Trans., Vol.135, pp. 35-51, 2023. https://doi.org/10.1016/j.isatra.2022.09.021
  19. [19] R. L. Sutherland, I. V. Kolmanovsky, A. R. Girard, F. A. Leve, and C. D. Petersen, “On closed-loop lyapunov stability with minimum-time MPC feedback laws for discrete-time systems,” 2019 IEEE 58th Conf. on Decision and Control (CDC), pp. 5231-5237, 2019. https://doi.org/10.1109/CDC40024.2019.9029869
  20. [20] L. Persson, A. Hansson, and B. Wahlberg, “An optimization algorithm based on forward recursion with applications to variable horizon MPC,” European J. of Control, Vol.75, Article No.100900, 2024. https://doi.org/10.1016/j.ejcon.2023.100900
  21. [21] W. B. Greer and S. Sultan, “Shrinking horizon model predictive control method for helicopter-ship touchdown,” J. of Guidance, Control, and Dynamics, Vol.43, No.5, pp. 884-900, 2020. https://doi.org/10.2514/1.G004374
  22. [22] F. Gao and W. Chen, “Mixed dissipativity control and disturbance rejection for singular systems,” J. Adv. Comput. Intell. Intell. Inform., Vol.27, No.4, pp. 720-725, 2023. https://doi.org/10.20965/jaciii.2023.p0720
  23. [23] J.-H. She, X. Xin, and Y. Pan, “Equivalent-input-disturbance approach-analysis and application to disturbance rejection in dual-stage feed drive control system,” IEEE/ASME Trans. on Mechatronics, Vol.16, No.2, pp. 330-340, 2011. https://doi.org/10.1109/TMECH.2010.2043258
  24. [24] Q. Mei, J. She, Z. Liu, and M. Wu, “Estimation and compensation of periodic disturbance using internal-model-based equivalent-input-disturbance approach,” Science China Information Sciences, Vol.65, No.8, Article No.182205, 2022. https://doi.org/10.1007/s11432-020-3192-5
  25. [25] K. Miyamoto, J. She, S. Nakano, D. Sato, and Y. Chen, “Active structural control of base-isolated building using equivalent-input-disturbance approach with reduced-order state observer,” J. of Dynamic Systems, Measurement, and Control, Vol.144, No.9, Article No.091006, 2022. https://doi.org/10.1115/1.4054819

Creative Commons License  This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.

*This site is desgined based on HTML5 and CSS3 for modern browsers, e.g. Chrome, Firefox, Safari, Edge, Opera.

Last updated on Jan. 21, 2026