Research Paper:
Spatial Incremental Model-Predictive Repetitive Control for Rotational Systems
Yujian Zhou*1,*2,*3
 , Jinhua She*1,*2,*3,*4,†
, Jinhua She*1,*2,*3,*4,†
 , Shijie Guo*5,*6
, Shijie Guo*5,*6
 , Feng Wang*1,*2,*3
, Feng Wang*1,*2,*3
 , Seiichi Kawata*1,*2,*3
, Seiichi Kawata*1,*2,*3
 , and Makoto Iwasaki*7
, and Makoto Iwasaki*7

*1School of Automation, China University of Geosciences
No.388 Lumo Road, Hongshan District, Wuhan, Hubei 430074, China
*2Hubei Key Laboratory of Advanced Control and Intelligent Automation for Complex Systems
No.388 Lumo Road, Hongshan District, Wuhan, Hubei 430074, China
*3Engineering Research Center of Intelligent Technology for Geo-Exploration, Ministry of Education
No.388 Lumo Road, Hongshan District, Wuhan, Hubei 430074, China
*4School of Engineering, Tokyo University of Technology
1404-1 Katakuramachi, Hachioji, Tokyo 192-0982, Japan
*5Engineering Research Center of the Ministry of Education for Intelligent Rehabilitation Equipment and Detection Technologies, Hebei Key Laboratory of Robot Sensing and Human-Robot Interaction
No.5340 Xiping Road, Beichen District, Tianjin 300401, China
*6School of Mechanical Engineering, Hebei University of Technology
No.5340 Xiping Road, Beichen District, Tianjin 300401, China
*7Department of Electrical and Mechanical Engineering, Nagoya Institute of Technology
Gokiso-cho, Showa-ku, Nagoya, Aichi 466-8555, Japan
†Corresponding author
This paper presents a spatial repetitive control method for precisely tracking a spatial periodic reference signal, achieved through incremental model-predictive control and an exact-feedback linearization method (IMPSRC) for rotational systems with disturbances. A modeling method in the spatial domain is first presented, followed by the configuration of the IMPSRC system. An exact-feedback-linearization controller is then designed to linearize the system model. Then we built an augmented system model using the dynamics of the tracking error of a spatial-domain periodic reference signal and the difference in the control input between two adjacent periods. The increment of the control input incorporates the internal model of the periodic reference signal, enabling the system to achieve tracking without steady-state error. An incremental model-predictive repetitive controller is then designed based on the augmented model. It enables precisely tracking spatial periodic signals and ensures stability under uncertainties and disturbances. The IMPSRC method is validated through simulations of tracking control of a rotational system. Spatial-domain sampling is triggered by the angular signal of the rotational system, which facilitates the implementation of the IMPSRC method. Simulation results show the effectiveness of the IMPSRC method.
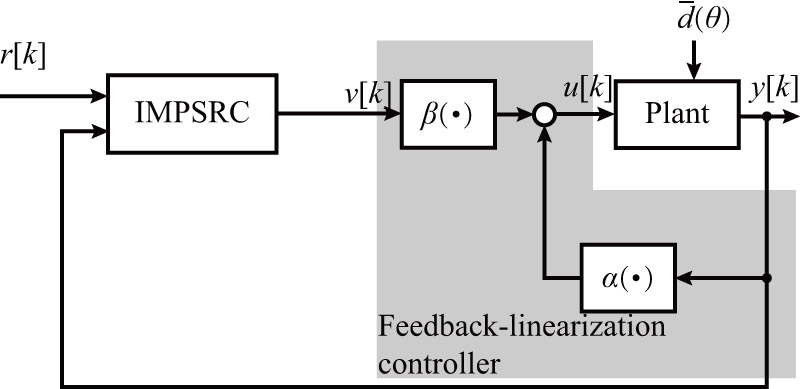
Configuration of the IMPSRC system
- [1] S. Hara, Y. Yamamoto, T. Omata, and M. Nakano, “Repetitive control system: A new type servo system for periodic exogenous signals,” IEEE Trans. on Automatic Control, Vol.33, No.7, pp. 659-668, 1988. https://doi.org/10.1109/9.1274
- [2] L. Zhou, D. Gao, and J. She, “Tracking control for a position-dependent periodic signal in a variable-speed rotational system,” Automatica, Vol.158, Article No.111282, 2023. https://doi.org/10.1016/j.automatica.2023.111282
- [3] P. Dini and S. Saponara, “Review on model based design of advanced control algorithms for cogging torque reduction in power drive systems,” Energies, Vol.15, No.23, Article No.8990, 2022. https://doi.org/10.3390/en15238990
- [4] M. Nakano, J.-H. She, Y. Matsuo, and T. Hino, “Elimination of position-dependent disturbances in constant-speed-rotation control systems,” Control Engineering Practice, Vol.4, No.9, pp. 1241-1248, 1996. https://doi.org/10.1016/0967-0661(96)00130-X
- [5] C.-L. Chen and Y.-H. Yang, “Position-dependent disturbance rejection using spatial-based adaptive feedback linearization repetitive control,” Int. J. of Robust and Nonlinear Control, Vol.19, No.12, pp. 1337-1363, 2009. https://doi.org/10.1002/rnc.1382
- [6] G. A. Ramos, J. Cortés-Romero, and H. Coral-Enriquez, “Spatial observer-based repetitive controller: An active disturbance rejection approach,” Control Engineering Practice, Vol.42, pp. 1-11, 2015. https://doi.org/10.1016/j.conengprac.2015.05.002
- [7] Q. Liu, X. Huo, K.-Z. Liu, and H. Zhao, “Accurate cycle aligned repetitive control for the rejection of spatially cyclic disturbances,” IEEE Trans. on Industrial Electronics, Vol.69, No.6, pp. 6173-6181, 2022. https://doi.org/10.1109/TIE.2021.3086705
- [8] R. S. Castro, J. V. Flores, and A. T. Salton, “Robust discrete-time spatial repetitive controller,” IEEE Trans. on Control Systems Technology, Vol.27, No.6, pp. 2696-2702, 2019. https://doi.org/10.1109/TCST.2018.2866978
- [9] X. Huo, M. Wang, K.-Z. Liu, and X. Tong, “Attenuation of position-dependent periodic disturbance for rotary machines by improved spatial repetitive control with frequency alignment,” IEEE/ASME Trans. on Mechatronics, Vol.25, No.1, pp. 339-348, 2020. https://doi.org/10.1109/TMECH.2019.2946675
- [10] L. Zhou, D. Gao, J. She, X.-M. Zhang, and H. Yan, “Adaptive spatial repetitive-control for time-varying periodic signals in a rotational system,” IEEE Trans. on Automatic Control, Vol.69, No.6, pp. 4134-4141, 2024. https://doi.org/10.1109/TAC.2023.3349316
- [11] L. Wang, “Model predicitive control system design and implementation using MATLAB®,” Springer, 2009. https://doi.org/10.1007/978-1-84882-331-0
- [12] B. A. Francis and W. M. Wonham, “The internal model principle of control theory,” Automatica, Vol.12, No.5, pp. 457-465, 1976. https://doi.org/10.1016/0005-1098(76)90006-6
- [13] Y. Liu, S. Cheng, B. Ning, and Y. Li, “Robust model predictive control with simplified repetitive control for electrical machine drives,” IEEE Trans. on Power Electronics, Vol.34, No.5, pp. 4524-4535, 2019. https://doi.org/10.1109/TPEL.2018.2857837
- [14] R. Cao and K.-S. Low, “A repetitive model predictive control approach for precision tracking of a linear motion system,” IEEE Trans. on Industrial Electronics, Vol.56, No.6, pp. 1955-1962, 2009. https://doi.org/10.1109/TIE.2008.2007034
- [15] E. R. C. Duque, A. Lunardi, J. S. Solís-Chaves, T. D. S. Paiva, D. A. Fernandes, and A. J. S. Filho, “Improvement of robustness of MPC adding repetitive behavior for the DFIG current control,” Energies, Vol.15, No.11, Article No.4114, 2022. https://doi.org/10.3390/en15114114
- [16] A. Isidori, “Nonlinear control systems,” 3rd Edition, Springer, 1995. https://doi.org/10.1007/978-1-84628-615-5
- [17] E. DiBenedetto, “Real analysis,” Springer, 2002.
- [18] Q. Mei, J. She, Z. Liu, and M. Wu, “Estimation and compensation of periodic disturbance using internal-model-based equivalent-input-disturbance approach,” Science China Information Sciences, Vol.65, No.8, Article No.182205, 2022. https://doi.org/10.1007/s11432-020-3192-5
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.