Research Paper:
Tsallis Entropy-Regularized Fuzzy Classification Maximum Likelihood Clustering with a t-Distribution
Yuta Suzuki and Yuchi Kanzawa†

Shibaura Institute of Technology
3-7-5 Toyosu, Koto-ku, Tokyo 135-8548, Japan
†Corresponding author
This study proposes a fuzzy clustering algorithm based on fuzzy classification maximum likelihood, t-distribution, and Tsallis entropy regularization. The proposed algorithm is shown to be a generalization of the two conventional algorithms, not only in the use of their objective functions, but also at their algorithmic level. The robustness of the proposed algorithm to outliers was confirmed in numerical experiments using an artificial dataset. In addition, experiments using 11 real datasets demonstrated the superiority of proposed algorithm in terms of the clustering accuracy.
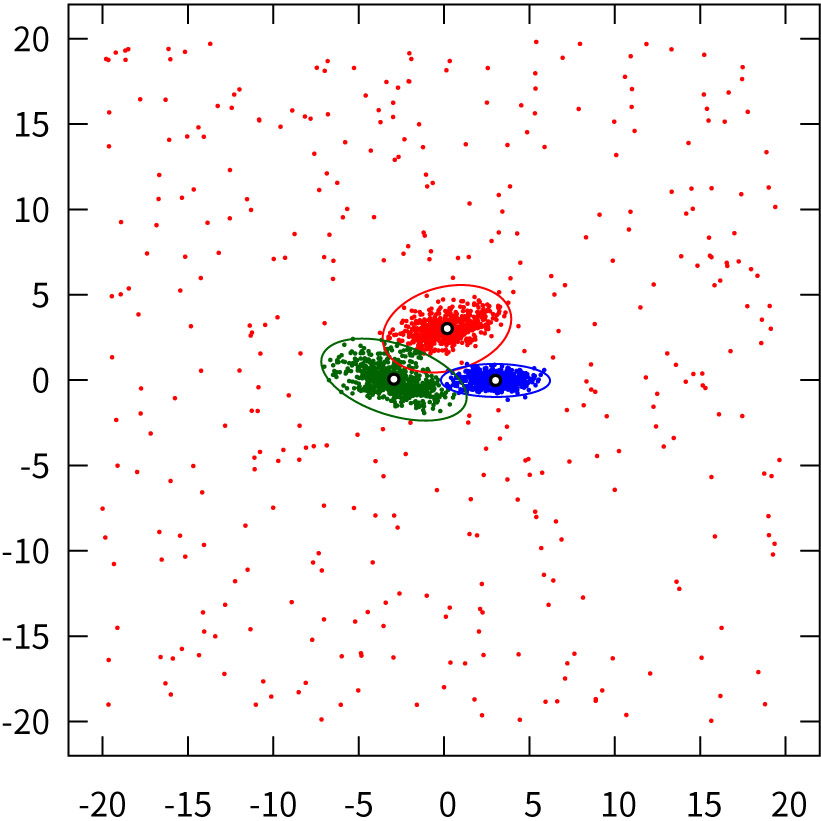
Clustering result obtained by T-FCMLT
- [1] J. Bezdek, “Pattern Recognition with Fuzzy Objective Function Algorithms,” Plenum Press, New York, 1981.
- [2] M. Ménard, V. Courboulay, and P.-A. Dardignac, “Possibilistic and Probabilistic Fuzzy Clustering: Unification within the Framework of the Nonextensive Thermostatistics,” Pattern Recognition, Vol.36, No.6, pp. 1325-1342, 2003. https://doi.org/10.1016/S0031-3203(02)00049-3
- [3] H. Ichihashi, K. Honda, and N. Tani, “Gaussian Mixture PDF Approximation and Fuzzy c-Means Clustering with Entropy Regularization,” Proc. 4th Asian Fuzzy System Symp., pp. 217-221, 2000.
- [4] M. S. Yang, C. Y. Lin, and Y. C. Tian, “Fuzzy Classification Maximum Likelihood Clustering with T-Distribution,” Applied Mechanics and Materials, Vol.598, pp. 392-397, 2014. https://doi.org/10.4028/www.scientific.net/AMM.598.392
- [5] W. Ali, I. Hussain, and M.-S. Yang, “Fuzzy Model-Based Robust Clustering with Multivariate t-Mixture Distributions,” Proc. of Int. Conf. on Computational Intelligence and Data Engineering, Vol.99, pp. 307-318, 2022. https://doi.org/10.1007/978-981-16-7182-1_25
- [6] C. Tsallis, “Possible Generalization of Boltzmann-Gibbs Statistics,” J. Statist. Phys., Vol.52, Nos.1-2, pp. 479-487, 1988. https://doi.org/10.1007/BF01016429
- [7] S. Miyamoto, H. Ichihashi, and K. Honda, “Algorithms for Fuzzy Clustering: Methods in c-Means Clustering with Applications,” Springer, 2008. https://doi.org/10.1007/978-3-540-78737-2
- [8] L. Hubert and P. Arabie, “Comparing Partitions,” J. of Classification, Vol.2, pp. 193-218, 1985. https://doi.org/10.1007/BF01908075
- [9] UCI homepage. https://archive.ics.uci.edu [Accessed December 24, 2023]
- [10] CRAN homepage. https://cran.r-project.org/index.html [Accessed December 24, 2023]
- [11] Y. Benjamini and Y. Hochberg, “Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing,” J. Roy. Statist. Soc. Ser. B (Methodological), Vol.57, No.1, pp. 289-300, 1995. https://doi.org/10.1111/j.2517-6161.1995.tb02031.x
- [12] U. J. Dang, R. P. Browne, and P. D. McNicholas, “Mixtures of Multivariate Power Exponential Distributions,” Biometrics, Vol.71, pp. 1081-1089, 2015. https://doi.org/10.1111/biom.12351
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.