Paper:
Differential Flatness-Based Parameter Estimation for Suspended Load Drones
Wataru Eikyu*, Kazuma Sekiguchi**
 , and Kenichiro Nonaka**
, and Kenichiro Nonaka**

*Graduate School of Integrative Science and Engineering, Tokyo City University
1-28-1 Tamazutsumi, Setagaya-ku, Tokyo 158-8557, Japan
**Department of Mechanical System Engineering, Faculty of Science and Engineering, Tokyo City University
1-28-1 Tamazutsumi, Setagaya-ku, Tokyo 158-8557, Japan
The transportation of goods by drones using cable towing has recently attracted considerable attention. When flying a suspended load drone, any discrepancy between the mathematical model and the actual drone deteriorates control performance. However, because some physical parameters are difficult to measure, creating an accurate mathematical model is extremely difficult. Therefore, we propose a parameter estimation method using differential flatness that can be extended for application to suspended load drones. This method overcomes the problem of dealing with higher-order derivatives of flat outputs and enables the estimation of physical parameters. In this study, we experimentally show that the proposed method improves trajectory tracking performance.
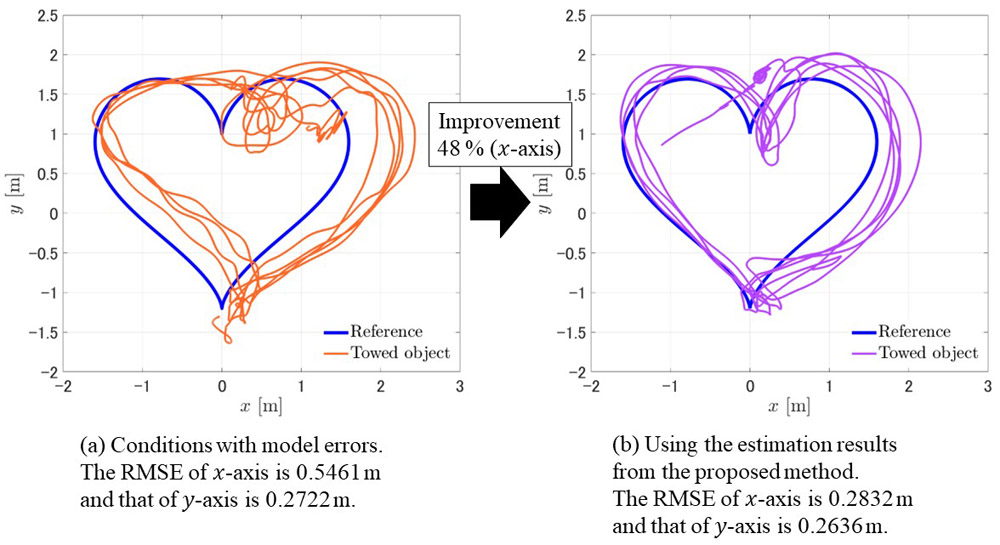
Trajectory of the towed object in the x-y plane
- [1] R. Ladig, H. Paul, R. Miyazaki, and K. Shimonomura, “Aerial Manipulation Using Multirotor UAV: A Review from the Aspect of Operating Space and Force,” J. Robot. Mechatron., Vol.33, No.2, pp. 196-204, 2021.
- [2] I. Palunko, P. Cruz, and R. Fierro, “Agile Load Transportation: Safe and Efficient Load Manipulation with Aerial Robots,” IEEE Robotics & Automation Magazine, Vol.19, No.3, pp. 69-79, 2012.
- [3] M. Fliess, J. Lévine, P. Martin, and P. Rouchon, “Flatness and Defect of Non-Linear Systems: Introductory Theory and Examples,” Int. J. of Control, Vol.61, No.6, pp. 1327-1361, 1995.
- [4] K. Sreenath, N. Michael, and V. Kumar, “Trajectory Generation and Control of a Quadrotor with a Cable-Suspended Load – A Differentially-Flat Hybrid System,” 2013 IEEE Int. Conf. on Robotics and Automation, pp. 4888-4895, 2013.
- [5] K. Sreenath, T. Lee, and V. Kumar, “Geometric Control and Differential Flatness of a Quadrotor UAV with a Cable-Suspended Load,” 52nd IEEE Conf. on Decision and Control, pp. 2269-2274, 2013.
- [6] P. Kotaru, G. Wu, and K. Sreenath, “Dynamics and Control of a Quadrotor with a Payload Suspended Through an Elastic Cable,” 2017 American Control Conf. (ACC), pp. 3906-3913, 2017.
- [7] F. A. Goodarzi, D. Lee, and T. Lee, “Geometric Stabilization of a Quadrotor UAV with a Payload Connected by Flexible Cable,” 2014 American Control Conf., pp. 4925-4930, 2014.
- [8] T. Lee, “Geometric Control of Multiple Quadrotor UAVs Transporting a Cable-Suspended Rigid Body,” 53rd IEEE Conf. on Decision and Control, pp. 6155-6160, 2014.
- [9] M. A. Kakanov, S. I. Tomashevich, V. S. Gromov, O. I. Borisov, F. B. Gromova, and A. A. Pyrkin, “Parameter Estimation of Quadrotor Model,” 2020 Int. Conf. Nonlinearity, Information and Robotics (NIR), pp. 1-5, 2020.
- [10] D. Ho, J. Linder, G. Hendeby, and M. Enqvist, “Mass Estimation of a Quadcopter Using IMU Data,” 2017 Int. Conf. on Unmanned Aircraft Systems (ICUAS), pp. 1260-1266, 2017.
- [11] S. Tang, V. Wüest, and V. Kumar, “Aggressive Flight with Suspended Payloads Using Vision-Based Control,” IEEE Robotics and Automation Letters, Vol.3, No.2, pp. 1152-1159, 2018.
- [12] V. Prkačin, I. Palunko, and I. Petrović, “State and Parameter Estimation of Suspended Load Using Quadrotor Onboard Sensors,” 2020 Int. Conf. on Unmanned Aircraft Systems (ICUAS), pp. 958-967, 2020.
- [13] R. Schenkendorf, U. Reichl, and M. Mangold, “Parameter Identification of Time-Delay Systems: A Flatness Based Approach,” IFAC Proc. Volumes, Vol.45, No.2, pp. 165-170, 2012.
- [14] J. Zeng and K. Sreenath, “Geometric Control of a Quadrotor with a Load Suspended from an Offset,” 2019 American Control Conf. (ACC), pp. 3044-3050, 2019.
- [15] W. Eikyu, K. Sekiguchi, and K. Nonaka, “Nonlinear Control for the Extended Model of the Load-Suspended UAV Based on the Experiments,” IFAC-PapersOnLine, Vol.54, No.14, pp. 90-95, 2021.
- [16] K. Sekiguchi, “Stabilization of Three-Link Acrobat via Hierarchical Linearization,” 54th IEEE Conf. on Decision and Control (CDC), pp. 7808-7813, 2015.
- [17] K. Sekiguchi, “Novel Control Method for Quadcopter-Hierarchical Linearization Approach,” 2017 11th Asian Control Conf. (ASCC), pp. 1853-1858, 2017.
- [18] K. Sekiguchi, W. Eikyu, and K. Nonaka, “Feedback Control for a Drone with Suspended Load via Hierarchical Linearization,” J. Robot. Mechatron., Vol.33, No.2, pp. 274-282, 2021.
- [19] A. Savitzky and M. J. E. Golay, “Smoothing and Differentiation of Data by Simplified Least Squares Procedures,” Analytical Chemistry, Vol.36, No.8, pp. 1627-1639, 1964.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.