Paper:
Repetitive Control Based on Multi-Stage PSO Algorithm with Variable Intervals for T–S Fuzzy Systems
Yibing Wang*,**, Manli Zhang*,**, Min Wu*,**,***,†, and Luefeng Chen*,**,***
*School of Automation, China University of Geosciences
No.388 Lumo Road, Hongshan, Wuhan 430074, China
**Hubei Key Laboratory of Advanced Control and Intelligent Automation for Complex Systems
No.388 Lumo Road, Hongshan, Wuhan 430074, China
***Engineering Research Center of Intelligent Technology for Geo-Exploration, Ministry of Education
No.388 Lumo Road, Hongshan, Wuhan 430074, China
†Corresponding author
This study presents a repetitive control method based on a multi-stage particle swarm optimization (PSO) algorithm with variable intervals to enhance the tracking performance of Takagi–Sugeno (T–S) fuzzy systems. First, a T–S fuzzy model is used to describe a nonlinear system. A modified repetitive control structure with two repetitive loops guarantees the tracking accuracy of periodic signals. Taking advantage of the two-dimensional (2D) property with continuous control and discrete learning, a continuous-discrete 2D model is presented to describe the nonlinear repetitive control system. Next, a multi-stage PSO algorithm with variable intervals searches for the best parameter combination in the linear matrix inequality-based stability condition to regulate the control and learning actions, which avoids a suboptimal solution and guarantees high control accuracy. Finally, an application to control the speed of synchronous motor with a permanent magnet demonstrates the validity of the method, and comparisons with related methods show its superiority.
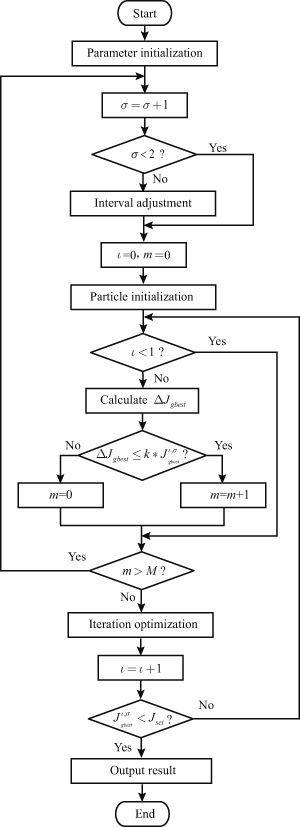
Flowchart of improved PSO algorithm
- [1] E. H. Copur, C. T. Freeman, B. Chu, and D. S. Laila, “Repetitive control of electrical stimulation for tremor suppression,” IEEE Trans. on Control Systems Technology, Vol.27, No.2, pp. 540-552, 2019.
- [2] L. Blanken, S. Koekebakker, and T. Oomen, “Multivariable repetitive control: decentralized designs with application to continuous media flow printing,” IEEE/ASME Trans. on Mechatronics, Vol.25, No.1, pp. 294-304, 2020.
- [3] T. Inoue, M. Nakano, T. Kubo, S. Matsumoto, and H. Baba, “High accuracy control of a proton synchrotron magnet power supply,” Proc. of the 8th Int. Federation of Automatic Control World Congress, Vol.14, No.2, pp. 3137-3142, 1981.
- [4] S. Hara, Y. Yamamoto, T. Omata, and M. Nakano, “Repetitive control system: a new type servo system for periodic exogenous signals,” IEEE Trans. on Automatic Control, Vol.33, No.7, pp. 659-668, 1988.
- [5] M. Wu, L. Zhou, and J. She, “Design of observer-based H∞ robust repetitive-control system,” IEEE Trans. on Automatic Control, Vol.56, No.6, pp. 1452-1457, 2011.
- [6] L. Zhou, J. She, M. Wu, and Y. He, “Design of robust observer-based modified repetitive-control system,” ISA Trans., Vol.52, No.3, pp. 375-382, 2013.
- [7] T. Takagi and M. Sugeno, “Fuzzy identification of systems and its applications to modeling and control,” IEEE Trans. on Systems, Man, and Cybernetics, Vol.15, No.1, pp. 116-132, 1985.
- [8] S. Tong, B. Huo, and Y. Li, “Observer-based adaptive decentralized fuzzy fault- tolerant control of nonlinear large-scale systems with actuator failures,” IEEE Trans. on Fuzzy Systems, Vol.22, No.1, pp. 1-15, 2014.
- [9] H. Zhang, J. Han, Y. Wang, and X. Liu, “Sensor fault estimation of switched fuzzy systems with unknown input,” IEEE Trans. on Fuzzy Systems, Vol.26, No.3, pp. 1114-1124, 2018.
- [10] Y. Wang, R. Wang, X. Xie, and H. Zhang, “Observer-based H∞ fuzzy control for modified repetitive control systems,” Neurocomputing, Vol.286, pp. 141-149, 2018.
- [11] R. Sakthivel, P. Selvaraj, and B. Kaviarasan, “Modified repetitive control design for nonlinear systems with time delay based on T–S fuzzy model,” IEEE Trans. on Systems, Man, and Cybernetics: Systems, Vol.50, No.2, pp. 646-655, 2020.
- [12] M. Zhang, M. Wu, L. Chen, and P. Yu, “Design of modified repetitive controller for T–S fuzzy systems,” J. Adv. Comput. Intell. Intell. Inform., Vol.23, No.3, pp. 602-610, 2019.
- [13] M. Zhang, M. Wu, L. Chen, S. Tian, and J. She, “Optimization of control and learning actions for repetitive-control system based on Takagi–Sugeno fuzzy model,” Int. J. of Systems Sciences, Vol.51, No.15, pp. 3030-3043, doi: 10.1080/00207721.2020.1807651, 2020.
- [14] H. B. Dong, D. J. Li, and X. P. Zhang, “A particle swarm optimization algorithm for dynamically adjusting inertia weights,” Computer Science, Vol.45, No.2, pp. 98-102, 2018.
- [15] W. Li and X. Chao, “Improved particles swarm optimization method for feature selection,” J. of Frontiers of Computer Science and Technology, Vol.13, No.6, pp. 990-1004, 2019.
- [16] K. Tanaka and H. O. Wang, “Fuzzy control systems design and analysis: a linear matrix inequality approach,” John Wiley & Sons, Inc., pp. 5-23, 2001.
- [17] J. She, M. Xie, D.-Y. Li, M. Wu, Z.-T. Liu, and W.-N. Zhang, “A VFF-RLS Method of Inertia Identification for PMSM,” IEEE Conf. on Control Technology and Applications (CCTA), pp. 942-943, 2019.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.