Top > JACIII > Suppression the Disturbance of Robotic Manipulators Based on N ...

single-jc.php

JACIII Vol.24 No.7 pp. 846-854
doi: 10.20965/jaciii.2020.p0846
(2020)

Paper:

Views over last 60 days: 481

Suppression the Disturbance of Robotic Manipulators Based on Nonlinear Disturbance Observer and Fuzzy Logic System

Wangyong He*,**,†, Haogui Li*,**, Yuanjiang Wang*,**, and Sanqiu Liu*,**

*School of Automation, China University of Geosciences
No.388 Lumo Road, Hongshan District, Wuhan, Hubei 430074, China

**Hubei Key Laboratory of Advanced Control and Intelligent Automation for Complex System
No.388 Lumo Road, Hongshan District, Wuhan, Hubei 430074, China

†Corresponding author

Received:
October 14, 2020
Accepted:
October 27, 2020
Published:
December 20, 2020
Creative Commons License
Keywords:
robotic manipulator, disturbances, nonlinear disturbance observer, fuzzy logic systems
Abstract

Robotic Manipulators (RM) are nonlinear and coupling system with time-variant and model uncertainties. In addition, RM are subject to different types of disturbances in practice, such as joint frictions, unknown payloads, and interferences from external systems. In this paper, these adverse factors are regarded as disturbance, and classifies them into internal disturbances and external disturbances. In order to achieve high-precision control, a Nonlinear Disturbance Observer (NDO) is designed to suppress external disturbances, and a Fuzzy Logic System (FLS) is designed to compensate internal disturbances. The scheme can effectively suppress the disturbance and improve the control accuracy. The validity of the scheme is shown by computer simulations of a two-link robot manipulator.

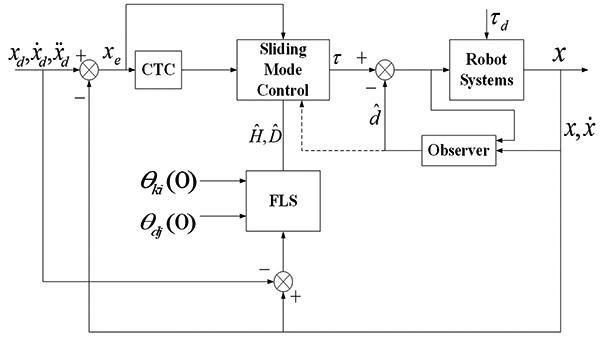
The control structure block diagram

The control structure block diagram

Cite this article as:
W. He, H. Li, Y. Wang, and S. Liu, “Suppression the Disturbance of Robotic Manipulators Based on Nonlinear Disturbance Observer and Fuzzy Logic System,” J. Adv. Comput. Intell. Intell. Inform., Vol.24 No.7, pp. 846-854, 2020.
Data files:
References
  1. [1] L.-X. Wang, “Stable adaptive fuzzy control of nonlinear systems,” IEEE Trans. on Fuzzy Systems, Vol.1, No.2, pp. 146-155, 1993.
  2. [2] B. Yoo and W. Ham, “Adaptive fuzzy sliding mode control of nonlinear system,” IEEE Trans. on Fuzzy Systems, Vol.6, No.2, pp. 315-321, 1998.
  3. [3] H. F. Ho, Y. K. Wong, and A. B. Rad, “Robust fuzzy tracking control for robotic manipulators,” Simulation Modelling Practice and Theory, Vol.15, Issue 7, pp. 801-816, 2007.
  4. [4] F. Piltan, A. Nabaee, M. M. Ebrahimi, and M. Bazregar, “Design Robust Fuzzy Sliding Mode Control Technique for Robot Manipulator Systems with Modeling Uncertainties,” Int. J. of Information Technology and Computer Science, Vol.5, No.8, pp. 123-135, 2013.
  5. [5] J. C. Wu and T. S. Liu, “A sliding-mode approach to fuzzy control design,” IEEE Trans. on Control Systems Technology, Vol.4, No.2, pp. 141-151, 1996.
  6. [6] R.-J. Lian, “Design of an enhanced adaptive self-organizing fuzzy sliding-mode controller for robotic systems,” Expert Systems with Applications, Vol.39, Issue 1, pp. 1545-1554, 2012.
  7. [7] S. Tong, T. Wang, Y. Li, and B. Chen, “A Combined Backstepping and Stochastic Small-Gain Approach to Robust Adaptive Fuzzy Output Feedback Control,” IEEE Trans. on Fuzzy Systems, Vol.21, No.2, pp. 314-327, 2013.
  8. [8] Y.-J. Liu and S. Tong, “Adaptive fuzzy control for a class of unknown nonlinear dynamical systems,” Fuzzy Sets and Systems, Vol.263, pp. 49-70, 2015.
  9. [9] Y. Li, S. Sui, and S. Tong, “Adaptive Fuzzy Control Design for Stochastic Nonlinear Switched Systems With Arbitrary Switchings and Unmodeled Dynamics,” IEEE Trans. on Cybernetics, Vol.47, No.2, pp. 403-414, 2017.
  10. [10] W.-H. Chen, D. J. Ballance, P. J. Gawthrop, and J. O’Reilly, “A nonlinear disturbance observer for robotic manipulators,” IEEE Trans. on Industrial Electronics, Vol.47, No.4, pp. 932-938, 2000.
  11. [11] A. Nikoobin and R. Haghighi, “Lyapunov-Based Nonlinear Disturbance Observer for Serial n-Link Robot Manipulators,” J. of Intelligent and Robotic Systems, Vol.55, Issues 2-3, pp. 135-153, 2009.
  12. [12] A. Mohammadi, M. Tavakoli, H. J. Marquez, and F. Hashemzadeh, “Nonlinear disturbance observer design for robotic manipulators,” Control Engineering Practice, Vol.21, Issue 3, pp. 253-267, 2013.
  13. [13] J. Yang, S. Li, and X. Yu, “Sliding-Mode Control for Systems With Mismatched Uncertainties via a Disturbance Observer,” IEEE Trans. on Industrial Electronics, Vol.60, No.1, pp. 160-169, 2013.
  14. [14] M. Chen and S. S. Ge, “Adaptive Neural Output Feedback Control of Uncertain Nonlinear Systems With Unknown Hysteresis Using Disturbance Observer,” IEEE Trans. on Industrial Electronics, Vol.62, No.12, pp. 7706-7716, 2015.
  15. [15] L.-X. Wang and J. M. Mendel, “Fuzzy basis functions, universal approximation, and orthogonal least-squares learning,” IEEE Trans. on Neural Networks, Vol.3, No.5, pp. 807-814, 1992.
  16. [16] M. W. Spong, S. Hutchinson, and M. Vidyasagar, “Robot Modeling and Control,” Industrial Robot, Vol.33, No.5, p. 403, 2006.
  17. [17] P. Gahinet, A. Nemirovskii, A. J. Laub, and M. Chilali, “The LMI control toolbox,” Proc. of the 1994 33rd IEEE Conf. on Decision and Control, Vol.3, pp. 2036-2041, 1994.
  18. [18] C.-Y. Su and T.-P. Leung, “A sliding mode controller with bound estimation for robot manipulators,” IEEE Trans. on Robotics and Automation, Vol.9, No.2, pp. 208-214, 1993.

Creative Commons License  This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.

*This site is desgined based on HTML5 and CSS3 for modern browsers, e.g. Chrome, Firefox, Safari, Edge, Opera.

Last updated on Apr. 22, 2024