Paper:
Noise Rejection Approaches for Various Rough Set-Based C-Means Clustering
Seiki Ubukata, Sho Sekiya, Akira Notsu, and Katsuhiro Honda
Osaka Prefecture University
1-1 Gakuen-cho, Nakaku, Sakai, Osaka 599-8531, Japan
In the field of cluster analysis, rough set-based extensions of hard C-means (HCM; k-means) including rough C-means (RCM), rough set C-means (RSCM), and rough membership C-means (RMCM) are promising approaches for dealing with the certainty, possibility, uncertainty of belonging of object to clusters. Since C-means-type methods are strongly affected by noise, noise clustering approaches have been proposed. In noise clustering approaches, noise objects, which are far from any cluster center, are rejected for robust estimation. In this paper, we introduce noise rejection approaches for rough set-based C-means based on probabilistic memberships and propose noise RCM with membership normalization (NRCM-MN), noise RSCM with membership normalization (NRSCM-MN), and noise RMCM (NRMCM). In addition, visualization demonstration of the cluster boundaries on the two-dimensional plane of the proposed methods is carried out to confirm the characteristics of each method. Furthermore, the clustering performance is verified by numerical experiments using real-world datasets.
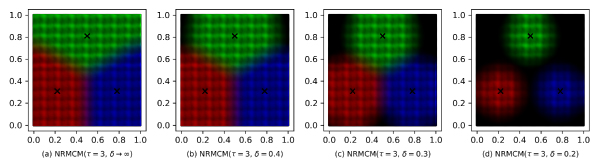
Cluster boundaries by noise RMCM
- [1] J. MacQueen, “Some Methods for Classification and Analysis of Multivariate Observations,” Proc. of the 5th Berkeley Symp. on Mathematical Statistics and Probability, pp. 281-297, 1967.
- [2] L. A. Zadeh, “Fuzzy sets,” Information and Control, Vol.8, Issue 3, pp. 338-353, 1965.
- [3] Z. Pawlak, “Rough sets,” Int. J. of Computer & Information Sciences, Vol.11, Issue 5, pp. 341-356, 1982.
- [4] Z. Pawlak, “Rough classification,” Int. J. of Man-Machine Studies, Vol.20, Issue 5, pp. 469-483, 1984.
- [5] Z. Pawlak, “Rough set approach to knowledge-based decision support,” European J. of Operational Research, Vol.99, Issue 1, pp. 48-57, 1997.
- [6] J. C. Bezdek, “Pattern Recognition with Fuzzy Objective Function Algorithms,” Plenum Press, 1981.
- [7] J. C. Dunn, “A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters,” J. of Cybernetics, Vol.3, Issue 3, pp. 32-57, 1973.
- [8] P. Lingras and C. West, “Interval Set Clustering of Web Users with Rough K-Means,” J. of Intelligent Information Systems, Vol.23, Issue 1, pp. 5-16, 2004.
- [9] G. Peters, “Some refinements of rough k-means clustering,” Pattern Recognition, Vol.39, Issue 8, pp. 1481-1491, 2006.
- [10] S. Ubukata, A. Notsu, and K. Honda, “General Formulation of Rough C-Means Clustering,” Int. J. of Computer Science and Network Security, Vol.17, No.9, pp. 29-38, 2017.
- [11] S. Ubukata, “A Unified Approach for Cluster-Wise and General Noise Rejection Approaches for K-Means Clustering,” PeerJ Computer Science, 5:e238, doi: 10.7717/peerj-cs.238, 2019.
- [12] S. Ubukata, A. Notsu, and K. Honda, “The Rough Set k-Means Clustering,” Proc. of 2016 Joint 8th Int. Conf. on Soft Computing and Intelligent Systems (SCIS) and 17th Int. Symp. on Advanced Intelligent Systems (ISIS), pp. 189-193, 2016.
- [13] S. Ubukata, A. Notsu, and K. Honda, “Characteristics of Rough Set C-Means Clustering,” J. Adv. Comput. Intell. Intell. Inform., Vol.22, No.4, pp. 551-564, 2018.
- [14] G. Peters, “Rough clustering utilizing the principle of indifference,” Information Sciences, Vol.277, pp. 358-374, 2014.
- [15] G. Peters, “Is there any need for rough clustering?,” Pattern Recognition Letters, Vol.53, pp. 31-37, 2015.
- [16] S. Ubukata, H. Kato, A. Notsu, and K. Honda, “Rough Set-Based Clustering Utilizing Probabilistic Memberships,” J. Adv. Comput. Intell. Intell. Inform., Vol.22, No.6, pp. 956-964, 2018.
- [17] S. Ubukata, A. Notsu, and K. Honda, “The Rough Membership k-Means Clustering,” Proc. of the 5th Int. Symp. on Integrated Uncertainty in Knowledge Modelling and Decision Making (IUKM 2016), pp. 207-216, 2016.
- [18] Z. Pawlak and A. Skowron, “Rough membership functions: a tool for reasoning with uncertainty,” C. Rauszer (Ed.), “Algebraic Methods in Logic and Computer Science,” Banach Center Publications, Vol.28, pp. 135-150, Institute of Mathematics, Polish Academy of Science, 1993.
- [19] Z. Pawlak and A. Skowron, “Rough membership functions,” R. R. Yager, J. Kacprzyk, and M. Fedrizzi (Eds.), “Advances in the Dempster-Shafer Theory of Evidence,” pp. 251-271, John Wiley & Sons, Inc., 1994.
- [20] R. N. Dave, “Characterization and detection of noise in clustering,” Pattern Recognition Letters, Vol.12, No.11, pp. 657-664, 1991.
- [21] R. N. Dave and R. Krishnapuram, “Robust clustering methods: a unified view,” IEEE Trans. on Fuzzy Systems, Vol.5, No.2, pp. 270-293, 1997.
- [22] S. Ubukata, S. Sekiya, A. Notsu, and K. Honda, “Noise Rejection Scheme for Rough Set-Based C-Means Clustering,” Proc. of 16th Int. Conf. on Modeling Decisions for Artificial Intelligence, pp. 70-81, 2019.
- [23] Q. Hu, D. Yu, and Z. Xie, “Neighborhood classifiers,” Expert Systems with Applications, Vol.34, Issue 2, pp. 866-876, 2008.
- [24] Q. Hu, D. Yu, J. Liu, and C. Wu, “Neighborhood rough set based heterogeneous feature subset selection,” Information Sciences, Vol.178, Issue 18, pp. 3577-3594, 2008.
- [25] Y. Y. Yao, “Generalized Rough Set Models,” L. Polkowski and A. Skowron (Eds.), “Rough Sets in Knowledge Discovery 1: Methodology and Applications,” pp. 286-318, Physica-Verlag, 1998.
- [26] UCI Machine Learning Repository, http://archive.ics.uci.edu/ml/ [accessed March 20, 2020]
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.