Top > JRM > System Identification Under Multirate Sensing Environments

single-rb.php

JRM Vol.37 No.5 pp. 1102-1112
doi: 10.20965/jrm.2025.p1102
(2025)

Paper:

Views over last 60 days: 85

System Identification Under Multirate Sensing Environments

Hiroshi Okajima ORCID Icon, Risa Furukawa, and Nobutomo Matsunaga ORCID Icon

Kumamoto University
2-39-1 Kurokami, Chuo-ku, Kumamoto, Kumamoto 860-8555, Japan

Received:
March 17, 2025
Accepted:
June 9, 2025
Published:
October 20, 2025
Creative Commons License
Keywords:
subspace identification, system identification, multirate system, cyclic reformulation, sensor fusion
Abstract

This paper proposes a system identification algorithm for systems with multirate sensors in a discrete-time framework. It is challenging to obtain an accurate mathematical model when the ratios of the inputs and outputs are different. A cyclic reformulation-based model for multirate systems is formulated, and the multirate system can be reduced to a linear time-invariant system to derive the model under the multirate sensing environment. The proposed algorithm integrates a cyclic reformulation with a state coordinate transformation of the cycled system to enable precise identification of systems under the multirate sensing environment. The effectiveness of the proposed system identification method is demonstrated through numerical simulations.

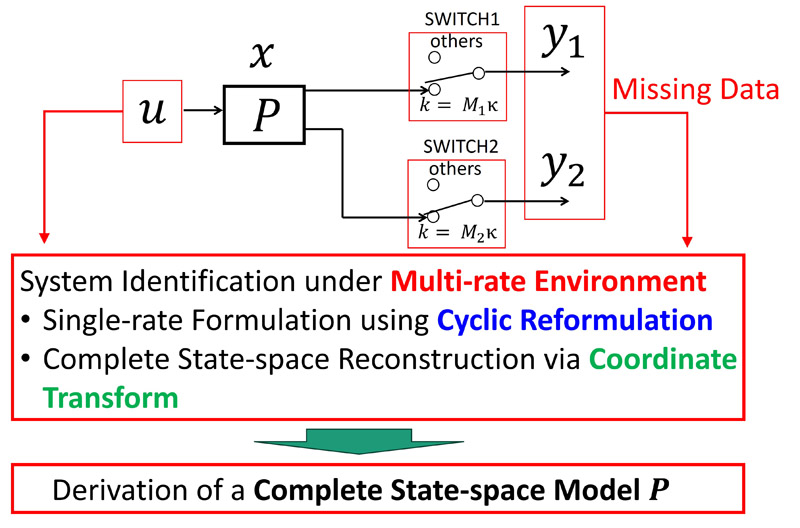
Multi-rate system identification sequence

Multi-rate system identification sequence

Cite this article as:
H. Okajima, R. Furukawa, and N. Matsunaga, “System Identification Under Multirate Sensing Environments,” J. Robot. Mechatron., Vol.37 No.5, pp. 1102-1112, 2025.
Data files:
References
  1. [1] L. Ljung, “System Identification: Theory for the User, 2nd Edition,” PTR Prentice Hall, 1998.
  2. [2] P. V. Overschee and B. D. Moor, “N4SID: Subspace algorithms for the identification of combined deterministic-stochastic systems,” Automatica, Vol.30, No.1, pp. 75-93, 1994. https://doi.org/10.1016/0005-1098(94)90230-5
  3. [3] D. Bauer and M. Jansson, “Analysis of the asymptotic properties of the MOESP type of subspace algorithms,” Automatica, Vol.36, No.4, pp. 497-509, 2000. https://doi.org/10.1016/S0005-1098(99)00174-0
  4. [4] H. Tanaka and K. Ikeda, “Identification of linear stochastic systems taking initial state into account,” 56th Annual Conf. of the Society of Instrument and Control Engineers, 2017. https://doi.org/10.1016/S0005-1098(99)00174-0
  5. [5] Y. Fujimoto, I. Maruta, and T. Sugie, “Input design for kernel-based system identification from the viewpoint of frequency response,” IEEE Trans. on Automatic Control, Vol.63, No.9, pp. 3075-3082, 2018. https://doi.org/10.1109/TAC.2018.2791464
  6. [6] I. Maruta and T. Sugie, “Closed-loop subspace identification for stable/ unstable systems using data compression and nuclear norm minimization,” IEEE Access, Vol.10, pp. 21412-21423, 2022. https://doi.org/10.1109/ACCESS.2022.3154017
  7. [7] J. Sjöberg, Q. Zhang, L. Ljung, A. Benveniste, B. Delyon, P.-Y. Glorennec, H. Hjalmarsson, and A. Juditsky, “Nonlinear black-box modeling in system identification: A unified overview,” Automatica, Vol.31, Issue 12, pp. 1691-1724, 1995. https://doi.org/10.1016/0005-1098(95)00120-8
  8. [8] F. Felici, J.-W. van Wingerden, and M. Verhaegen, “Subspace identification of MIMO LPV systems using a periodic scheduling sequence,” Automatica, Vol.43, No.10, pp. 1684-1697, 2007. https://doi.org/10.1016/j.automatica.2007.02.027
  9. [9] M. Yin, A. Iannelli, and R. S. Smith, “Subspace identification of linear time-periodic systems with periodic inputs,” IEEE Control Systems Letters, Vol.5, No.1, pp. 145-150, 2021. https://doi.org/10.1109/LCSYS.2020.3000950
  10. [10] D. Karlsson and D. J. Hill, “Modelling and identification of nonlinear dynamic loads in power systems,” IEEE Trans. on Power Systems, Vol.9, Issue 1, pp. 157-166, 1994. https://doi.org/10.1109/59.317546
  11. [11] I. S. Apostolakis, “An estimation algorithm for multirate sampled digital control systems,” Int. J. of Control, Vol.56, Issue 4, pp. 813-830, 1992. https://doi.org/10.1080/00207179208934345
  12. [12] W. Lu, D. G. Fisher, and S. L. Shah, “Multirate constrained adaptive control,” Int. J. of Control, Vol.51, No.6, pp. 1439-1456, 1990. https://doi.org/10.1080/00207179008934145
  13. [13] R. Scattolini, “Multi-rate self-tuning predictive controller for multi-variable systems,” Int. J. of Systems Science, Vol.23, Issue 8, pp. 1347-1359, 1992. https://doi.org/10.1080/00207729208949388
  14. [14] T. Sato, “Parametric Design of a Dual-Rate Controller for Improvement in Steady-State Intersample Response,” SICE J. of Control, Measurement, and System Integration, Vol.1, Issue 4, pp. 329-334, 2008. https://doi.org/10.9746/jcmsi.1.329
  15. [15] Y. Minami, H. Okajima, K. Sawada, and K. Sekiguchi, “Special Issue on Navigation and Control Technologies for Autonomous Mobility,” J. Robot. Mechatron., Vol.35, No.2, pp. 229-230, 2023. https://doi.org/10.20965/jrm.2023.p0229
  16. [16] N. Matsunaga, I. Yamamoto, and H. Okajima, “Navigation System for Personal Mobility Vehicles Following a Cluster of Pedestrians in a Corridor Using Median of Candidate Vectors Observer,” J. Robot. Mechatron., Vol.35, No.6, pp. 1562-1572, 2023. https://doi.org/10.20965/jrm.2023.p1562
  17. [17] N. Matsunaga, K. Murata, and H. Okajima, “Robust Cooperative Transport System with Model Error Compensator Using Multiple Robots with Suction Cups,” J. Robot. Mechatron., Vol.35, No.6, pp. 1583-1592, 2023. https://doi.org/10.20965/jrm.2023.p1583
  18. [18] D. J. Yeong, G. V. Hernandez, J. Barry, and J. Walsh, “Sensor and Sensor Fusion Technology in Autonomous Vehicles: A Review,” Sensors, Vol.21, No.6, Article No.2140, 2021. https://doi.org/10.3390/s21062140
  19. [19] Y. Kanuki, N. Ohta, and N. Nakazawa, “Development of autonomous moving robot using appropriate technology for Tsukuba Challenge,” J. Robot. Mechatron., Vol.35, No.2, pp. 279-287, 2023. https://doi.org/10.20965/jrm.2023.p0279
  20. [20] Q. M. Shao and A. Cinar, “System identification and distributed control for multi-rate sampled systems,” J. of Process Control, Vol.34, pp. 1-12, 2015. https://doi.org/10.1016/j.jprocont.2015.06.010
  21. [21] F. Ding and T. Chen, “Performance analysis of multi-innovation gradient type identification methods,” Automatica, Vol.43, No.1, pp. 1-14, 2007. https://doi.org/10.1016/j.automatica.2006.07.024
  22. [22] J. Wang, T. Chen, and B. Huang, “Identification of Multirate Sampled-Data Systems,” IFAC Proc. Volumes, Vol.37, Issue 1, pp. 149-154, 2004. https://doi.org/10.1016/S1474-6670(17)38723-2
  23. [23] D. Li, S. L. Shah, T. Chen, and R. Patwardhan, “System identification and long-range predictive control of multi-rate systems,” Proc. of the 1999 American Control Conf., 1999.
  24. [24] H. Okajima, Y. Fujimoto, H. Oku, and H. Kondo, “Cyclic Reformulation Based System Identification for Periodically Time-varying Systems,” IEEE Access, Vol.13, pp. 26483-26493, 2025. https://doi.org/10.1109/ACCESS.2025.3537086
  25. [25] S. Bittanti and P. Colaneri, “Invariant representations of discrete-time periodic systems,” Automatica, Vol.36, Issue 12, pp. 1777-1793, 2000. https://doi.org/10.1016/S0005-1098(00)00087-X
  26. [26] S. Bittanti and P. Colaneri, “Periodic systems: Filtering and control,” Springer-Verlag, London, 2009. https://doi.org/10.1007/978-1-84800-911-0
  27. [27] H. Okajima, Y. Hosoe, and T. Hagiwara, “State observer under multi-rate sensing environment and its design using l2-induced norm,” IEEE Access, Vol.11, pp. 20079-20087, 2023. https://doi.org/10.1109/ACCESS.2023.3249187
  28. [28] H. Okajima, K. Arinaga, and A. Hayashida, “Design of Observer-Based Feedback Controller for Multi-Rate Systems with Various Sampling Periods Using Cyclic Reformulation,” IEEE Access, Vol.11, pp. 121956-121965, 2023. https://doi.org/10.1109/ACCESS.2023.3329117

Creative Commons License  This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.

*This site is desgined based on HTML5 and CSS3 for modern browsers, e.g. Chrome, Firefox, Safari, Edge, Opera.

Last updated on Oct. 19, 2025