Paper:
Local Minimum Avoidance in Potential Field Method Through Virtual-Wall Generation and Wall Following
Hanwool Woo
 and Seiya Hirota
and Seiya Hirota
Department of Mechanical Systems Engineering, Faculty of Engineering, Kogakuin University
2665-1 Nakano-machi, Hachioji, Tokyo 192-0015, Japan
This paper proposes a novel method to solve the local minimum problem of conventional potential field methods by generating virtual walls to achieve autonomous movement in unknown environments. The existence of local minimum can be attributed to two main factors: (i) the robot enters a concave region and becomes trapped, and (ii) the attractive and repulsive forces balance out when an obstacle is located directly in the direction of the goal. The proposed method addresses these challenges by generating a virtual wall along obstacles with concave shapes, preventing the robot from entering such regions. Furthermore, when a local minimum occurs owing to the force equilibrium caused by obstacles in the goal direction, the robot executes a wall-following behavior to escape from the local minimum. We confirmed that the proposed method enables a robot to move toward the goal more efficiently than the conventional method by generating virtual walls and following them in an environment with local minimum.
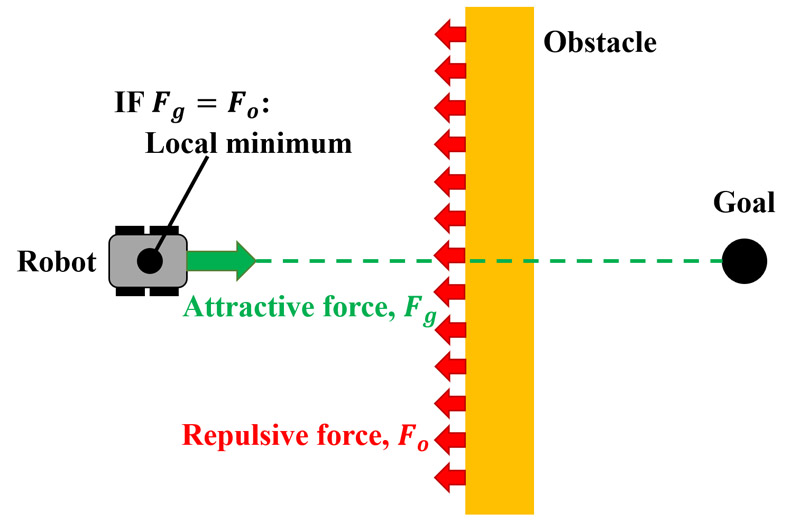
Local minimum problem with the artificial potential field method
- [1] O. Khatib, “Real-time obstacle avoidance for manipulators and mobile robots,” The Int. J. of Robotics Research, Vol.5, No.1, pp. 90-98, 1986.
- [2] P. Khosla and R. Volpe, “Superquadric Artificial Potentials for Obstacle Avoidance and Approach,” Proc. of IEEE Int. Conf. on Robotics and Automation, Vol.3, pp. 1778-1784, 1988. https://doi.org/10.1109/ROBOT.1988.12323
- [3] F. Janabi-Sharifi and D. Vinke, “Integration of the artificial potential field approach with simulated annealing for robot path planning,” Proc. of 8th IEEE Int. Symp. on Intelligent Control, pp. 536-541, 1993. https://doi.org/10.1109/ISIC.1993.397640
- [4] Z. Wu, J. Dai, B. Jiang, and H. R. Karimi, “Robot path planning based on artificial potential field with deterministic annealing,” ISA Trans., Vol.138, pp. 74-87, 2023. https://doi.org/10.1016/j.isatra.2023.02.018
- [5] N. S. F. Doria, E. O. Freire, and J. C. Basilio, “An algorithm inspired by the deterministic annealing approach to avoid local minimum in artificial potential fields,” Proc. of 16th Int. Conf. on Advanced Robotics (ICAR), 2013. https://doi.org/10.1109/ICAR.2013.6766480
- [6] T. Zhang, Y. Zhu, and J. Song, “Real-time motion planning for mobile robots by means of artificial potential field method in unknown environment,” Industrial Robot, Vol.37, Issue 4, pp. 384-400, 2010. https://doi.org/10.1108/01439911011044840
- [7] J. Kim, S. Park, W. Lee, W. Kim, N. Doh, and C. Nam, “Escaping Local Minima: Hybrid Artificial Potential Field with Wall-Follower for Decentralized Multi-Robot Navigation,” arXiv preprint, arXiv:2409.10332, 2024. https://doi.org/10.48550/arXiv.2409.10332
- [8] Y. Chen, G. Bai, Y. Zhan, X. Hu, and J. Liu, “Path Planning and Obstacle Avoiding of the USV Based on Improved ACO-APF Hybrid Algorithm with Adaptive Early-Warning,” IEEE Access, Vol.9, pp. 40728-40742, 2021. https://doi.org/10.1109/ACCESS.2021.3062375
- [9] B. Guo, Z. Kuang, J. Guan, M. Hu, L. Rao, and X. Sun, “An Improved A-Star Algorithm for Complete Coverage Path Planning of Unmanned Ships,” Int. J. of Pattern Recognition and Artificial Intelligence, Vol.36, No.3, Article No.2259009, 2022. https://doi.org/10.1142/S0218001422590091
- [10] G. Tang, C. Tang, C. Claramunt, X. Hu, and P. Zhou, “Geometric A-Star Algorithm: An Improved A-Star Algorithm for AGV Path Planning in a Port Environment,” IEEE Access, Vol.9, pp. 59196-59210, 2021. https://doi.org/10.1109/ACCESS.2021.3070054
- [11] S. Rodriguez, X. Tang, J.-M. Lien, and N. M. Amato, “An obstacle-based rapidly-exploring random tree,” Proc. of 2006 IEEE Int. Conf. on Robotics and Automation, pp. 895-900, 2006. https://doi.org/10.1109/ROBOT.2006.1641823
- [12] B. Li and B. Chen, “An Adaptive Rapidly-Exploring Random Tree,” IEEE/CAA J. of Automatica Sinica, Vol.9, Issue 2, pp. 283-294, 2022. https://doi.org/10.1109/JAS.2021.1004252
- [13] L. I. Meng, D. B. Wang, and T. T. Bai, “UAV Route Planning Based on Ant Colony Optimization and Artificial Potential,” J. of Applied Sciences, Vol.30, No.2, pp. 215-220, 2012.
- [14] M. A. K. Jaradat, M. H. Garibeh, and E. A. Feilat, “Autonomous mobile robot dynamic motion planning using hybrid fuzzy potential field,” Soft Computing, Vol.16, pp. 153-164, 2012. https://doi.org/10.1007/s00500-011-0742-z
- [15] R. Zhang, L. Zhou, and Z. Liu, “Dynamic Path Planning for Mobile Robot Based on RRT* and Dynamic Window Approach,” J. of System Simulation, Vol.36, Issue 4, pp. 957-968, 2024. https://doi.org/10.16182/j.issn1004731x.joss.22-1543
- [16] J. Hou, W. Jiang, Z. Luo, L. Yang, X. Hu, and B. Guo, “Dynamic Path Planning for Mobile Robots by Integrating Improved Sparrow Search Algorithm and Dynamic Window Approach,” Actuators, Vol.13, Issue 1, Article No.24, 2024. https://doi.org/10.3390/act13010024
- [17] W. J. Yim and J. B. Park, “Analysis of Mobile Robot Navigation Using Vector Field Histogram According to the Number of Sectors, the Robot Speed and the Width of the Path,” Proc. of the 2014 Int. Conf. on Control, Automation and Systems (ICCAS 2014), 2024. https://doi.org/10.1109/ICCAS.2014.6987943
- [18] M. Srinivasan and S. Coogan, “Control of Mobile Robots Using Barrier Functions Under Temporal Logic Specifications,” arXiv preprint, arXiv:1908.04903, 2019. https://doi.org/10.48550/arXiv.1908.04903
- [19] C. Peng, O. Donca, and A. Hereid, “Safe Path Planning for Polynomial Shape Obstacles via Control Barrier Functions and Logistic Regression,” arXiv preprint, arXiv:2210.03704, 2022. https://doi.org/10.48550/arXiv.2210.03704
- [20] S. Amertet and G. Gebresenbet, “Collision Avoidance for Wheeled Mobile Robots in Smart Agricultural Systems Using Control Barrier Function Quadratic Programming,” Applied Sciences, Vol.15, Issue 5, Article No.2450, 2025. https://doi.org/10.3390/app15052450
- [21] M. H. Mabrouk and C. R. McInnes, “Solving the potential field local minimum problem using internal agent states,” Robotics and Autonomous Systems, Vol.56, Issue 12, pp. 1050-1060, 2008. https://doi.org/10.1016/j.robot.2008.09.006
- [22] R. Kubo, K. Yamamoto, and A. Themelis, “Deadlock avoidance for robot navigation with potential field method in an unknown environment,” Proc. of the 65th Japan Joint Automatic Control Conf., pp. 8-13, 2022 (in Japanese). https://doi.org/10.11511/jacc.65.0_8
- [23] B. P. Gerkey, R. T. Vaughan, and A. Howard, “The player/stage project: Tools for multi-robot and distributed sensor systems,” Proc. of the Int. Conf. on Advanced Robotics, pp. 317-323, 2003.
- [24] B. P. Gerkey, R. T. Vaughan, K. Støy, A. Howard, G. Sukhatme, and M. J. Matarić, “Most valuable player: A robot device server for distributed control,” IEEE/RSJ Int. Conf. on Intelligent Robots and Systems. Expanding the Societal Role of Robotics in the the Next Millennium, pp. 1226-1231, 2001. https://doi.org/10.1109/IROS.2001.977150
- [25] R. T. Vaughan, B. P. Gerkey, and A. Howard, “On device abstractions for portable, reusable robot code,” IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS 2003), pp. 2121-2427, 2003. https://doi.org/10.1109/IROS.2003.1249233
- [26] J. Kerr and K. Nickels, “Robot operating systems: Bridging the gap between human and robot,” Proc. of the 2012 44th Southeastern Symp. on System Theory (SSST), pp. 99-104, 2012. https://doi.org/10.1109/SSST.2012.6195127
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.