Research Paper:
Tsallis Entropy-Regularized Yang-Type Fuzzy c-Hidden Markov Models
Tomoki Nomura and Yuchi Kanzawa

Shibaura Institute of Technology
3-7-5 Toyosu, Koto-ku, Tokyo 135-8548, Japan
This study proposes Tsallis entropy-regularized Yang-type fuzzy c-hidden Markov models (TYFCHMMs), a fuzzy clustering algorithm based on hidden Markov model (HMM), for series data. First, the relationship between a Gaussian mixture model with identity covariances, which is a conventional probabilistic clustering algorithm for vectorial data, and Yang-type fuzzy c-means, which is a conventional fuzzy clustering algorithm for vectorial data, is determined. Second, the relationship between Bezdek-type fuzzy c-means and Tsallis entropy-regularized fuzzy c-means, which are two conventional fuzzy clustering algorithms for vectorial data, is determined. Based on these relationships, TYFCHMMs are constructed from mixtures of HMMs (MoHMMs), which are conventional probabilistic clustering algorithms based on HMM for series data, using Yang-type fuzzification and Tsallis entropy regularization. Through numerical tests using an artificial dataset, the effects of parameters on the clustering results of TYFCHMMs and the close relationship between TYFCHMMs and MoHMMs are identified. Furthermore, numerical tests using ten real datasets confirmed that TYFCHMMs outperform MoHMMs in terms of clustering accuracy.
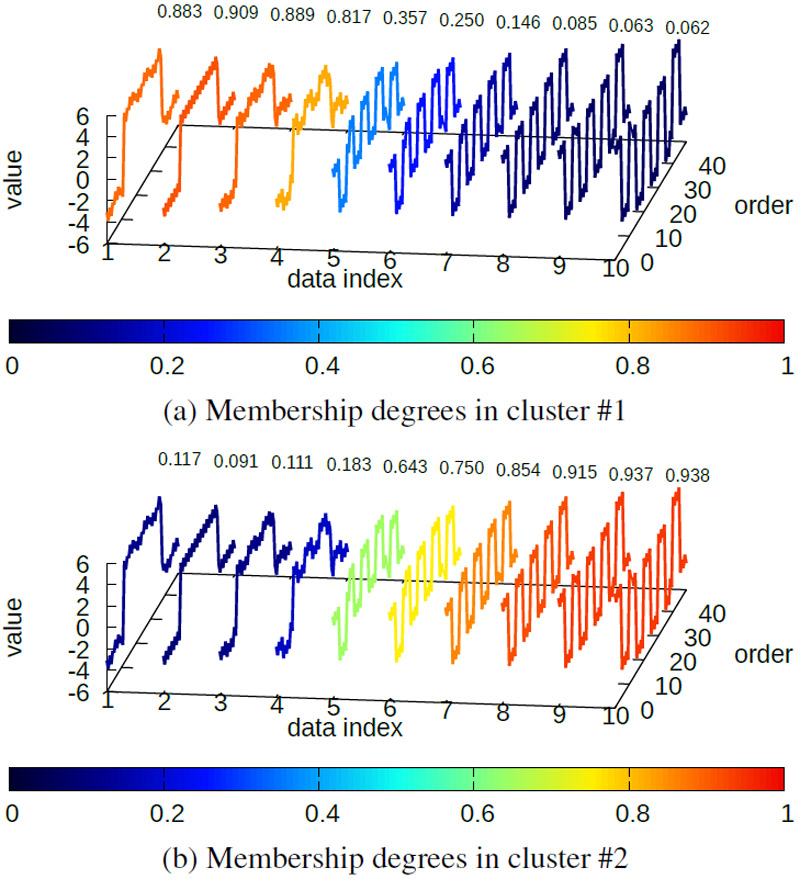
Membership degrees of TYFCHMMs (𝑚,𝜆,𝜆′)=(1.15,100000,1)
- [1] J. C. Bezdek, “Pattern Recognition with Fuzzy Objective Function Algorithms,” Plenum Press, New York, 1981.
- [2] M. Yasuda, “Tsallis Entropy Based Fuzzy c-means Clustering with Parameter Adjustment,” Proc. SCIS&ISIS2012, pp. 1534-1539, 2012. https://doi.org/10.1109/SCIS-ISIS.2012.6505118
- [3] M.-S. Yang, “On a class of fuzzy classification maximum likelihood procedures,” Fuzzy Sets and Systems, Vol.57, No.3, pp. 365-375, 1993. https://doi.org/10.1016/0165-0114(93)90030-L
- [4] P. D’Urso, “Fuzzy clustering for data time arrays with inlier and outlier time trajectories,” IEEE Trans. on Fuzzy Systems, Vol.13, No.5, pp. 583-604, 2005. https://doi.org/10.1109/TFUZZ.2005.856565
- [5] C. Serantoni, A. Riente, A. Abeltino, G. Bianchetti, M. M. De Giulio, S. Salini, A. Russo, F. Landi, M. De Spirito, and G. Maulucci, “Integrating dynamic time warping and K-means clustering for enhanced cardiovascular fitness assessment,” Biomedical Signal Processing and Control, Vol.97, Article No.106677, 2024. https://doi.org/10.1016/j.bspc.2024.106677
- [6] S. H. Holan and N. Ravishanker, “Time series clustering and classification via frequency domain methods,” Wiley Interdisciplinary Reviews: Computational Statistics, Vol.10, Issue 6, Article No.e1444, 2018. https://doi.org/10.1002/wics.1444
- [7] J. Kreienkamp, M. Agostini, R. Monden, K. Epstude, P. de Jonge, and L. F. Bringmann, “A Gentle Introduction and Application of Feature-Based Clustering with Psychological Time Series,” Multivariate Behavioral Research, Vol.60, Issue 2, pp. 362-392, 2025. https://doi.org/10.1080/00273171.2024.2432918
- [8] Y. Xiong and D.-Y. Yeung, “Mixtures of ARMA Models for Model-Based Time Series Clustering,” Proc. of ICDM2002, pp. 717-720, 2002. https://doi.org/10.1109/ICDM.2002.1184037
- [9] J. Alon, S. Sclaroff, G. Kollios, and V. Pavlovic, “Discovering clusters in motion time-series data,” Proc. IEEE Computer Society Conf. on Computer Vision and Pattern Recognition, Vol.1, pp. 375-381, 2003. https://doi.org/10.1109/CVPR.2003.1211378
- [10] C. Tsallis, “Possible Generalization of Boltzmann–Gibbs Statistics,” J. of Statistical Physics, Vol.52, Nos.1-2, pp. 479-487, 1988. https://doi.org/10.1007/BF01016429
- [11] L. E. Baum, T. Petrie, G. Soules, and N. Weiss, “A maximization technique occurring in the statistical analysis of probabilistic functions of Markov chains,” The Annals of Mathematical Statistics, Vol.41, No.1, pp. 164-171, 1970. https://doi.org/10.1214/aoms/1177697196
- [12] R. Umatani, T. Imai, K. Kawamoto, and S. Kunimasa, “Time Series Clustering with an EM algorithm for Mixtures of Linear Gaussian State Space Models,” Pattern Recognition, Vol.138, Article No.109375, 2023. https://doi.org/10.1016/j.patcog.2023.109375
- [13] K. Kalpakis, “Mining of Science Time-Series Data” https://redirect.cs.umbc.edu/kalpakis/TS-mining/ [Accessed January 28, 2024]
- [14] H. A. Dau, E. Keogh, K. Kamgar, C.-C. M. Yeh, Y. Zhu, S. Gharghabi C. A. Ratanamahatana, Y. Chen, B. Hu, N. Begum, A. Bagnall, A. Mueen, G. Batista, and Hexagon-ML, “The UCR Time Series Classification Archive.” https://www.cs.ucr.edu/eamonn/time_series_data_2018/ [Accessed December 12, 2021]
- [15] B. V. Kini and C. C. Sekhar, “Bayesian mixture of AR models for time series clustering,” Pattern Analysis and Applications, Vol.16, No.2, pp. 179-200, 2013. https://doi.org/10.1007/s10044-011-0247-5
- [16] L. Hubert and P. Arabie, “Comparing Partitions,” J. of Classification, Vol.2, No.1, pp. 193-218, 1985. https://doi.org/10.1007/BF01908075
- [17] M. Ren, Z. Wang, and J. Jiang, “A Self-Adaptive FCM for the Optimal Fuzzy Weighting Exponent,” Int. J. of Computational Intelligence and Applications, Vol.18, No.2, Article No.1950008, 2019. https://doi.org/10.1142/S1469026819500081
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.