Research Paper:
Exploring Model Structures to Reduce Data Requirements for Neural ODE Learning in Control Systems
Takanori Hashimoto
 , Nobuyuki Matsui, Naotake Kamiura
, Nobuyuki Matsui, Naotake Kamiura
 , and Teijiro Isokawa
, and Teijiro Isokawa

Graduate School of Engineering, University of Hyogo
2167 Shosha, Himeji, Hyogo 671-2280, Japan
In this study, we investigate model structures for neural ODEs to improve the data efficiency in learning the dynamics of control systems. We introduce two model structures and compare them with a typical baseline structure. The first structure considers the relationship between the coordinates and velocities of the control system, while the second structure adds linearity with respect to the control term to the first structure. Both of these structures can be easily implemented without requiring additional computation. In numerical experiments, we evaluate these structure on simulated simple pendulum and CartPole systems and show that incorporating these characteristics into the model structure leads to accurate learning with a smaller amount of training data compared to the baseline structure.
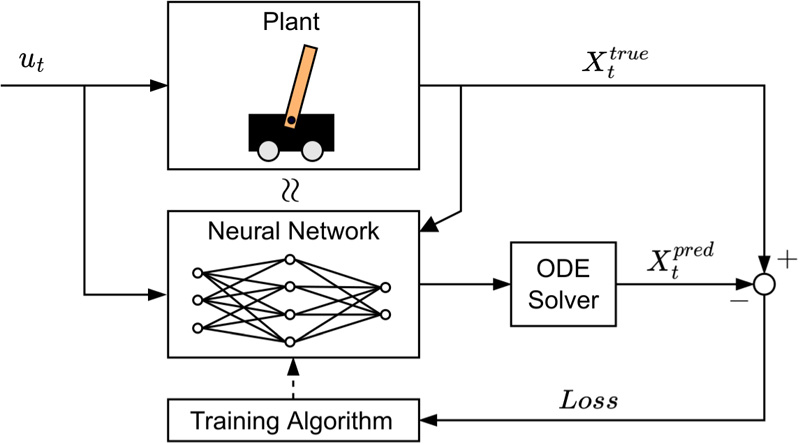
Neural ODEs approximation of system dynamics
- [1] L. Lennart, “System identification,” A. Procházka, J. Uhlíř, P. W. J. Rayner, and N. G. Kingsbury (Eds.), “Signal Analysis and Prediction,” pp. 163-173, Springer-Verlag, 1998.
- [2] W. Khalil and E. Dombre, “Modeling, Identification and Control of Robots,” Elsevier, 2014.
- [3] S. L. Brunton, J. L. Proctor, and J. N. Kutz, “Discovering Governing Equations from Data by Sparse Identification of Nonlinear Dynamical Systems,” Proc. of the National Academy of Sciences, Vol.113, No.15, pp. 3932-3937, 2016. https://doi.org/10.1073/pnas.1517384113
- [4] P. M. Wensing, S. Kim, and J.-J. E. Slotine, “Linear Matrix Inequalities for Physically Consistent Inertial Parameter Identification: A Statistical Perspective on the Mass Distribution,” IEEE Robotics and Automation Letters, Vol.3, No.1, pp. 60-67, 2017. https://doi.org/10.1109/LRA.2017.2729659
- [5] V. M. M. Alvarez, R. Roşca, and C. G. Fălcuţescu, “Dynode: Neural ordinary differential equations for dynamics modeling in continuous control,” arXiv:2009.04278, 2020. https://doi.org/10.48550/arXiv.2009.04278
- [6] C. Yildiz, M. Heinonen, and H. Lähdesmäki, “Continuous-time model-based reinforcement learning,” Int. Conf. on Machine Learning, pp. 12009-12018, 2021.
- [7] S. Greydanus, M. Dzamba, and J. Yosinski, “Hamiltonian neural networks,” Advances in Neural Information Processing Systems 32 (NeurIPS 2019), 2019.
- [8] Y. D. Zhong, B. Dey, and A. Chakraborty, “Symplectic Ode-Net: Learning Hamiltonian Dynamics with Control,” Proc. of the 8th Int. Conf. on Learning Representations (ICLR 2020), 2019.
- [9] A. Sosanya and S. Greydanus, “Dissipative Hamiltonian Neural Networks: Learning Dissipative and Conservative Dynamics Separately,” arXiv:2201.10085, 2022. https://doi.org/10.48550/arXiv.2201.10085
- [10] M. Cranmer, S. Greydanus, S. Hoyer, P. Battaglia, D. Spergel, and S. Ho, “Lagrangian neural networks,” arXiv:2003.04630, 2020. https://doi.org/10.48550/arXiv.2003.04630
- [11] M. A. Roehrl, T. A. Runkler, V. Brandtstetter, M. Tokic, and S. Obermayer, “Modeling system dynamics with physics-informed neural networks based on lagrangian mechanics,” IFAC-PapersOnLine, Vol.53, No.2, pp. 9195-9200, 2020. https://doi.org/10.1016/j.ifacol.2020.12.2182
- [12] R. T. Q. Chen, Y. Rubanova, J. Bettencourt, and D. K. Duvenaud, “Neural ordinary differential equations,” Advances in Neural Information Processing Systems 31 (NeurIPS 2018), 2018.
- [13] L. S. Pontryagin, “Mathematical theory of optimal processes,” CRC Press, 1987.
- [14] P. J. Davis and P. Rabinowitz, “Methods of numerical integration,” Courier Corporation, 2007.
- [15] C. Tsitouras, “Runge–Kutta pairs of order 5(4) satisfying only the first column simplifying assumption,” Computers & Mathematics with Applications, Vol.62, No.2, pp. 770-775, 2011. https://doi.org/10.1016/j.camwa.2011.06.002
- [16] D. P. Kingma and J. Ba, “Adam: A method for stochastic optimization,” arXiv:1412.6980, 2014. https://doi.org/10.48550/arXiv.1412.6980
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.