Top > JACIII > Generalization of Tsallis Entropy-Based Fuzzy c-Means Clusteri ...

single-jc.php

JACIII Vol.26 No.6 pp. 884-892
doi: 10.20965/jaciii.2022.p0884
(2022)

Paper:

Views over last 60 days: 293

Generalization of Tsallis Entropy-Based Fuzzy c-Means Clustering and its Behavior at the Infinity Point

Yuchi Kanzawa* and Sadaaki Miyamoto**

*Shibaura Institute of Technology
3-7-5 Toyosu, Koto-ku, Tokyo 135-8548, Japan

**University of Tsukuba
1-1-1 Tennodai, Tsukuba, Ibaraki 305-8573, Japan

Received:
March 19, 2022
Accepted:
June 5, 2022
Published:
November 20, 2022
Creative Commons License
Keywords:
Tsallis entropy-based fuzzy c-means clustering, fuzzy classification function
Abstract

This study presents a generalized Tsallis entropy-based fuzzy c-means (GTFCM) clustering algorithm. Furthermore, the results of this study show that the behavior of GTFCM, at an infinity point of the fuzzy classification function, is similar to that of some conventional clustering algorithms. This result implies that such behavior is determined by a certain part of the GTFCM objective function.

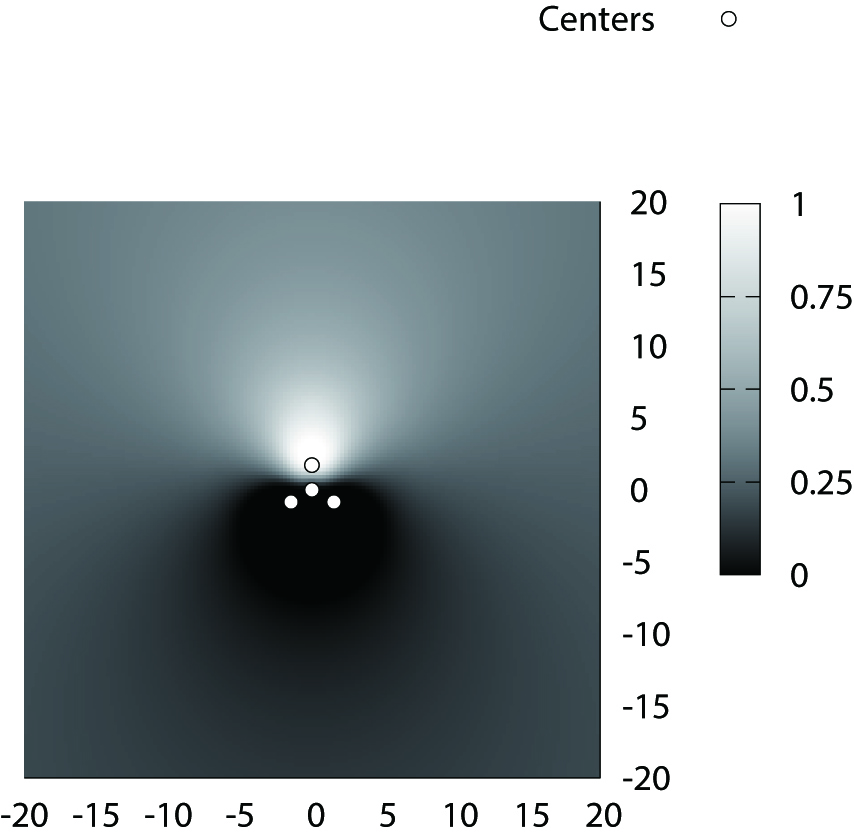
FCF example of GTFCM

FCF example of GTFCM

Cite this article as:
Y. Kanzawa and S. Miyamoto, “Generalization of Tsallis Entropy-Based Fuzzy c-Means Clustering and its Behavior at the Infinity Point,” J. Adv. Comput. Intell. Intell. Inform., Vol.26 No.6, pp. 884-892, 2022.
Data files:
References
  1. [1] J. C. Bezdek, “Pattern Recognition with Fuzzy Objective Function Algorithms,” Springer New York, NY, 1981.
  2. [2] J. B. MacQueen, “Some Methods of Classification and Analysis of Multivariate Observations,” Proc. 5th Berkeley Symp. on Math. Stat. and Prob., pp. 281-297, 1967.
  3. [3] K. Treerattanapitak and C. Jaruskulchai, “Membership Enhancement with Exponential Fuzzy Clustering for Collaborative Filtering,” Lecture Notes in Computer Science, Vol.6443, pp. 559-566, 2010.
  4. [4] S. Miyamoto and M. Mukaidono, “Fuzzy c-Means as a Regularization and Maximum Entropy Approach,” Proc. 7th Int. Fuzzy Systems Association World Congress (IFSA’97), pp. 86-92, 1997.
  5. [5] S. Miyamoto and K. Umayahara, “Fuzzy Clustering by Quadratic Regularization,” Proc. 1998 IEEE Int. Conf. Fuzzy Syst., pp. 1394-1399, 1998.
  6. [6] Y. Kanzawa, “Generalization of Quadratic Regularized and Standard Fuzzy c-Means Clustering with respect to Regularization of Hard c-Means,” Lecture Notes in Computer Science, Vol.8234, pp. 152-165, 2013.
  7. [7] M. Ménard, V. Courboulay, and P.-A. Dardignac, “Possibilistic and Probabilistic Fuzzy Clustering: Unification Within the Framework of the Non-Extensive Thermostatistics,” Pattern Recogn., Vol.36, No.6, pp. 1325-1342, 2003.
  8. [8] S. Miyamoto and K. Umayahara, “Methods in Hard and Fuzzy Clustering,” Z.-Q. Liu and S. Miyamoto (Eds.), “Soft Computing and Human-Centered Machines,” pp. 85-129, Springer, Tokyo, 2000.
  9. [9] Y. Kanzawa and S. Miyamoto, “Regularized Fuzzy c-Means Clustering and its Behavior at Point of Infinity,” J. Adv. Comput. Intell. Intell. Inform., Vol.23, No.3, pp. 485-492, 2019.
  10. [10] Y. Kanzawa and S. Miyamoto, “Generalized Fuzzy c-Means Clustering and its Property of Fuzzy Classification Function,” J. Adv. Comput. Intell. Intell. Inform., Vol.25, No.1, pp. 73-82, 2021.
  11. [11] S. Miyamoto, H. Ichihashi, and K. Honda, “Algorithms for Fuzzy Clustering: Methods in c-Means Clustering with Applications,” Springer Berlin, Heidelberg, 2008.
  12. [12] S. Miyamoto and N. Kurosawa, “Controlling Cluster Volume Sizes in Fuzzy c-Means Clustering,” Proc. SCIS&ISIS 2004, pp. 1-4, 2004.
  13. [13] H. Ichihashi, K. Honda, and N. Tani, “Gaussian Mixture PDF Approximation and Fuzzy c-Means Clustering with Entropy Regularization,” Proc. 4th Asian Fuzzy System Symp., pp. 217-221, 2000.
  14. [14] I. S. Dhillon and D. S. Modha, “Concept Decompositions for Large Sparse Text Data Using Clustering,” Machine Learning, Vol.42, pp. 143-175, 2001.
  15. [15] S. Miyamoto and K. Mizutani, “Fuzzy Multiset Model and Methods of Nonlinear Document Clustering for Information Retrieval,” Lecture Notes in Computer Science, Vol.3131, pp. 273-283, 2004.
  16. [16] K. Mizutani, R. Inokuchi, and S. Miyamoto, “Algorithms of Nonlinear Document Clustering Based on Fuzzy Multiset Model,” Int. J. of Intelligent Systems, Vol.23, No.2, pp. 176-198, 2008.
  17. [17] Y. Kanzawa, “On Kernelization for a Maximizing Model of Bezdek-Like Spherical Fuzzy c-Means Clustering,” Lecture Notes in Computer Science, Vol.8825, pp. 108-121, 2014.
  18. [18] Y. Kanzawa, “A Maximizing Model of Bezdek-Like Spherical Fuzzy c-Means,” J. Adv. Comput. Intell. Intell. Inform., Vol.19, No.5, pp. 662-669, 2015.
  19. [19] Y. Kanzawa, “A Maximizing Model of Spherical Bezdek-Type Fuzzy Multi-Medoids Clustering,” J. Adv. Comput. Intell. Intell. Inform., Vol.19, No.6, pp. 738-746, 2015.
  20. [20] C.-H. Oh, K. Honda, and H. Ichihashi, “Fuzzy Clustering for Categorical Multivariate Data,” Proc. 9th IFSA World Congress and 20th NAFIPS Int. Conf., pp. 2154-2159, 2001.
  21. [21] K. Honda, S. Oshio, and A. Notsu, “FCM-type fuzzy co-clustering by K-L information regularization,” Proc. of 2014 IEEE Int. Conf. on Fuzzy Systems, pp. 2505-2510, 2014.
  22. [22] K. Honda, S. Oshio, and A. Notsu, “Item Membership Fuzzification in Fuzzy Co-Clustering Based on Multinomial Mixture Concept,” Proc. of 2014 IEEE Int. Conf. on Granular Computing (GrC), pp. 94-99, 2014.
  23. [23] Y. Kanzawa, “Fuzzy Co-Clustering Algorithms Based on Fuzzy Relational Clustering and TIBA Imputation,” J. Adv. Comput. Intell. Intell. Inform., Vol.18, No.2, pp. 182-189, 2014.
  24. [24] Y. Kanzawa, “On Possibilistic Clustering Methods Based on Shannon/Tsallis-Entropy for Spherical Data and Categorical Multivariate Data,” Lecture Notes in Computer Science, Vol.9321, pp. 115-128, 2015.
  25. [25] Y. Kanzawa, “Bezdek-Type Fuzzified Co-Clustering Algorithm,” J. Adv. Comput. Intell. Intell. Inform., Vol.19, No.6, pp. 852-860, 2015.

Creative Commons License  This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.

*This site is desgined based on HTML5 and CSS3 for modern browsers, e.g. Chrome, Firefox, Safari, Edge, Opera.

Last updated on Apr. 19, 2024