Paper:
Design of Modified Repetitive Controller for T–S Fuzzy Systems
Manli Zhang*,**, Min Wu*,**,†, Luefeng Chen*,**, and Pan Yu**,***
*School of Automation, China University of Geosciences
No.388 Lumo Road, Hongshan District, Wuhan 430074, China
**Hubei Key Laboratory of Advanced Control and Intelligent Automation for Complex Systems
No.388 Lumo Road, Hongshan District, Wuhan 430074, China
***Department of Electrical and Electronic Engineering, Chiba University
1-33 Yayoi, Inage, Chiba 263-8522, Japan
†Corresponding author
A repetitive controller contains a pure-delay positive-feedback loop that makes it difficult to stabilize a strictly proper system. A low-pass filter is inserted in a repetitive controller to relax the stability condition of the modified repetitive-control system at the cost of degrading the tracking performance. In this study, a modified repetitive-control approach is developed, which reaches a balance between the stability and tracking performance for a class of affine nonlinear systems based on the Takagi–Sugeno fuzzy model. First, a 2D model is established to adjust continuous control and discrete learning actions preferentially induced by exploiting the 2D property in a repetitive-control process. Then, the Lyapunov stability theory and 2D system theory are used to derive a sufficient stability condition in the form of linear matrix inequalities to design parallel-distributed-compensation-based state-feedback controllers. Finally, an application-oriented example is used, and a comparison is performed to show that an extra variable is introduced such that the developed method has a better tracking performance.
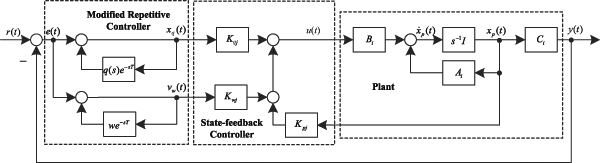
A new configuration of repetitive controller for T?S fuzzy systems
- [1] P. Tomei and C. M. Verrelli, “Linear repetitive learning controls for nonlinear systems by Padé approximants,” Int. J. of Adaptive Control and Signal Processing, Vol.29, No.6, pp. 783-804, 2015.
- [2] C. Luo, J. Yao, F. Chen et al., “Adaptive repetitive control of hydraulic load simulator with RISE feedback,” IEEE Access, Vol.5, pp. 23901-23911, 2017.
- [3] M. Nakano, T. Inoue, and Y. Yamamoto, “Repetitive control,” Central South University of Technology Press, pp. 18-82, 1994.
- [4] B. A. Francis and W. M. Wonham, “The internal model principle of control theory,” Automatica, Vol.12, No.5, pp. 457-465, 1976.
- [5] S. Hara, Y. Yamamoto, T. Omata et al., “Repetitive control system: a new type servo system for periodic exogenous signals,” IEEE Trans. on Automatic Control, Vol.33, No.7, pp. 659-668, 1988.
- [6] L. Zhou, J. H. She, M. Wu et al., “Design of robust observer-based modified repetitive control system,” ISA Trans., Vol.52, No.3, pp. 375-382, 2013.
- [7] M. Wu, L. Zhou, and J. H. She, “Design of observer-based H∞ robust repetitive control system,” IEEE Trans. on Automatic Control, Vol.56, No.6, pp. 1452-1457, 2011.
- [8] R. Sakthivel, P. Selvaraj, and B. Kaviarasan, “Modified repetitive control design for nonlinear systems with time delay based on T–S fuzzy model,” IEEE Trans. on Systems, Man, and Cybernetics: Systems, doi: 10.1109/TSMC.2017.2756912, 2017.
- [9] X.-M. Sun, S.-L. Du, P. Shi et al., “Input-to-state stability for nonlinear systems with large delay periods based on switching techniques,” IEEE Trans. on Circuits and Systems I: Regular Papers, Vol.61, No.6, pp. 1789-1800, 2014.
- [10] Y. Yang and J. M. Lee, “A switching robust model predictive control approach for nonlinear systems,” J. of Process Control, Vol.23, No.6, pp. 852-860, 2013.
- [11] T. Takagi and M. Sugeno, “Fuzzy identification of systems and its applications to modeling and control,” IEEE Trans. on Systems, Man, and Cybernetics, Vol.15, No.1, pp. 116-132, 1985.
- [12] K. Tanaka, “Stability analysis of fuzzy systems using Lyapunov’s direct method,” North American Fuzzy Information Processing Society, pp. 133-136, 1990.
- [13] B. Sharma and Zaheeruddin, “Design & analysis of fuzzy logic controller using Lyapunov function for a non-linear system,” India Int. Conf. on Power Electronics 2010, pp. 1-5, 2011.
- [14] D. Y. Kim, B. P. Jin, and Y. H. Joo, “Output feedback stabilization condition for nonlinear systems using artificial T–S fuzzy model,” Int. Conf. on Control, Automation and Systems, pp. 96-100, 2012.
- [15] M. Hamdy and P. Hamdan, “Robust fuzzy output feedback controller for affine nonlinear systems via T–S fuzzy bilinear model: CSTR benchmark,” ISA Trans., Vol.57, pp. 85-92, 2015.
- [16] M. L. Zhang, M. Wu, L. F. Chen et al., “A new modified repetitive control system design based on T–S fuzzy model,” Proc. of the 12nd China-Japan Int. Workshop on Information Technology and Control Applications, 2018.
- [17] P. Yu, M. Wu, J. H. She et al., “Robust repetitive control and disturbance rejection based on two-dimensional model and equivalent-input-disturbance approach,” Asian J. of Control, Vol.18, No.6, pp. 2325-2335, 2016.
- [18] J. H. She, M. Wu, Y. H. Lan et al., “Simultaneous optimisation of the low-pass filter and state-feedback controller in a robust repetitive-control system,” IET Control Theory & Applications, Vol.4. No.8, pp. 1366-1376, 2010.
- [19] J. H. She, M. X. Fang, Y. Ohyama et al., “Improving disturbance-rejection performance based on an equivalent-input-disturbance approach,” IEEE Trans. on Industrial Electronics, Vol.55, No.1, pp. 380-389, 2008.
- [20] Y. C. Wang, R. Wang, X. Xie et al., “Observer-based H∞ fuzzy control for modified repetitive control systems,” Neurocomputing, Vol.286, pp. 141-149, 2018.
- [21] Y. Yamamoto, “A function space approach to sampled data control systems and tracking problems,” IEEE Trans. on Automatic Control, Vol.39, No.4, pp. 703-713, 1994.
- [22] P. P. Khargonekar, I. R. Petersen, and K. Zhou, “Robust stabilization of uncertain linear systems: quadratic stabilizability and H∞ control theory,” IEEE Trans. on Automatic Control, Vol.35, No.3, pp. 356-361, 1990.
- [23] Y. Zheng and G. R. Chen, “Fuzzy impulsive control of chaotic systems based on TS fuzzy mode,” Chaos, Solitons & Fractals, Vol.39, No.4, pp. 2002-2011, 2009.
- [24] G. B. Koo, J. B. Park, and Y. H. Joo, “Decentralized sampled-data fuzzy observer design for nonlinear interconnected system,” IEEE Trans. on Fuzzy Systems, Vol.24, No.3, pp. 661-674, 2016.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.